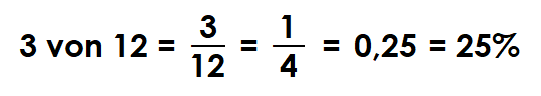R6 Tabellenkalkulation - Prozentrechnen

>>> R6 Tabellenkalkulation

Das Prozentrechnen hat in der Tabellenkalkulation so seinen eigenen Stil. Wenn man sich dran gewöhnt hat, dann ist es sogar einfacher als die Sichtweise der 6. Klasse, in der Ihr das Prozentrechnen gelernt habt. Aber es verlangt Euch wieder einmal ein bisserl Umgewöhnen ab:

Zunächst ist ein Prozentsatz eine Art (neben 3 anderen Arten!), einen Anteil auszudrücken, den ein Teil in einem Ganzen einnimmt:

Beispiel: In einer Schülergruppe aus 12 Schüler sind 3 Mädchen. Auf die Frage "Wie hoch ist der Anteil der Mädchen?" oder "wie viel ist 3 von 12?" habt Ihr in der 6. Klasse 4 verschiedene mögliche Antworten gelernt:

1. Bruchteil

Wohl in der ersten Mathestunde in der 6. Klasse war die Antwort: Bei 12 Schüler ist eine Schülerin ein Zwölftel (früher: der zwölfte Teil). 3 Schülerinnen sind dann 3 mal ein Zwölftel, also drei Zwölftel, anschaulich:

Bei der Antwort "3 von 12 ist 3 Zwölftel" muss man im Übrigen nichts rechnen! Man nennt einfach den Bruch: Teil/Ganzes.

2. Vereinfachter/gekürzter Bruchteil

Drei Wochen später habt Ihr gelernt, dass man das Kästchenmuster auch als Nebeneinander von 4 Spalten sehen kann. Die Mädchen sind dann eine Spalte von 4 also ein Viertel. Der Anteil 1/4 ist also gleich bedeutende mit 3/12. Ihr habt gelernt Bruchteile so einfach wie möglich anzugeben. Ihr habt gelernt zu kürzen.

3. Dezimaler Anteil

Wieder ein paar Wochen später habt Ihr gelernt, den Anteil am dezimalen Meterstab zu veranschaulichen:

Ihr habt gelernt, den Bruchstrich als "geteilt durch" zu sehen und habt durch die schriftliche Teilung die Zahl 0,25 erhalten. Sie drückt am Meterstab aus, wie groß der Anteil der Mädchen ist. Die ganze Gruppe ist die 1!

4. Prozentualer Anteil

Wieder ein paar Wochen später habt Ihr gelernt, den Anteil am Meterstab zu veranschaulichen, wobei Ihr Euch das Ganze nicht mehr als 1 sondern als 100% vorgestellt habt:

Das hat den Vorteil, dass man nicht so kleine 0,....-Zahlen hat sondern Zahlen, die man sich besser merken kann.

TIPP:

Stell Dir mal vor bei der Wahl in Höslwang würde man den Anteil der Grünen bei der Bundestagswahl (351 von 1047 Stimmen) als Bruchteil oder dezimal veröffentlichen! :-)

In der Tabellenkalkulation ...

... rechnest Du nichts weiter als Teil/Ganzes und wählst die Anzeigeform nur durch die Formatierung!