Matheprojekt: Würfel färben 1*6: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | [[Datei:rubik1.png|miniatur|RUBIK-Würfelchen]] | + | [[Datei:rubik1.png|miniatur|'''Abb1:''' RUBIK-Würfelchen]] |
| − | [[Datei:warum729.png|miniatur|Abb2: Warum gibt es 729 Färbungen?]] | + | [[Datei:warum729.png|miniatur|'''Abb2:''' Warum gibt es 729 Färbungen?]] |
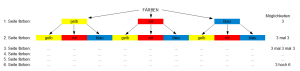
| − | Einen Würfel mit drei Farben anzumalen (sagen wir in rot-gelb-blau), ist sicherlich nicht schwer. Da man dabei 6 mal die Entscheidung hat, ihn rot, gelb oder blau anzumalen, geht das zunächst mal auf $$3^6=729$$ verschiedene Arten, vorausgesetzt, man hat die Freiheit, jede Farbe beliebig oft benutzen zu können oder nicht, es also auch einfarbige Würfel geben darf. | + | Einen Würfel mit drei Farben anzumalen (sagen wir in rot-gelb-blau), ist sicherlich nicht schwer. Da man dabei 6 mal die Entscheidung hat, ihn rot, gelb oder blau anzumalen, geht das zunächst mal auf $$3^6=729$$ verschiedene Arten, vorausgesetzt, man hat die Freiheit, jede Farbe beliebig oft benutzen zu können oder nicht, es also auch einfarbige Würfel geben darf. Wenn das nicht klar ist, mal die Abb2 rechts ansehen! ;-) |
| − | Da aber jeder Mensch Würfel als ''eigentlich gleich gefärbt'' betrachtet, wenn sie sich nur durch Drehung voneinander unterscheiden, sind es ''eigentlich'' viel weniger als 729. Da die Klassen in diesem Sinne gleicher Würfel aber unterschiedlich groß sind, lässt sich der Nachteil dieses kombinatorischen Ansatzes nicht so leicht heilen! | + | Da aber jeder Mensch Würfel als '''eigentlich gleich gefärbt''' betrachtet, wenn sie sich nur durch Drehung voneinander unterscheiden, sind es '''eigentlich''' viel weniger als 729. Da die Klassen in diesem Sinne gleicher Würfel aber unterschiedlich groß sind, lässt sich der Nachteil dieses kombinatorischen Ansatzes nicht so leicht heilen! |
Eine Technik der Mathematik, solche Probleme zu lösen, ist die '''Klassifikation''' aller Würfel in Typen, die durch '''drehinvariante Eigenschaften''' beschrieben werden. Dazu ein einfaches Beispiel: | Eine Technik der Mathematik, solche Probleme zu lösen, ist die '''Klassifikation''' aller Würfel in Typen, die durch '''drehinvariante Eigenschaften''' beschrieben werden. Dazu ein einfaches Beispiel: | ||
| Zeile 41: | Zeile 41: | ||
####Typ: '''U + V + ein einzelnes''' in '''6''' Farbvarianten, z.B. [[Datei:Josef2.png]] | ####Typ: '''U + V + ein einzelnes''' in '''6''' Farbvarianten, z.B. [[Datei:Josef2.png]] | ||
###Die 3 gleichfarbigen haben Hut-Form | ###Die 3 gleichfarbigen haben Hut-Form | ||
| − | ####Typ: '''Hut + V + ein einzelnes''' in ''' | + | ####Typ: '''Hut + V + ein einzelnes''' in '''?''' Farbvarianten, z.B. [[Datei:Olaf.png]] |
##Seitenflächenfarbenverteilung: 2|2|2 | ##Seitenflächenfarbenverteilung: 2|2|2 | ||
###Typ: '''Alle gleichfarbigen gegenüber''', da gibt es nur '''eine''' Farbvariation, [[Datei:Kinglui.png]] | ###Typ: '''Alle gleichfarbigen gegenüber''', da gibt es nur '''eine''' Farbvariation, [[Datei:Kinglui.png]] | ||
| Zeile 47: | Zeile 47: | ||
###Typ: '''V + V + V''' in '''?''' Farbvarianten, z.B. [[Datei:god.png]] | ###Typ: '''V + V + V''' in '''?''' Farbvarianten, z.B. [[Datei:god.png]] | ||
| − | Insgesamt also | + | Insgesamt also 48 + ? |
'''Viel Spaß beim Denken!''' | '''Viel Spaß beim Denken!''' | ||
Aktuelle Version vom 30. Oktober 2022, 16:00 Uhr
Einen Würfel mit drei Farben anzumalen (sagen wir in rot-gelb-blau), ist sicherlich nicht schwer. Da man dabei 6 mal die Entscheidung hat, ihn rot, gelb oder blau anzumalen, geht das zunächst mal auf $$3^6=729$$ verschiedene Arten, vorausgesetzt, man hat die Freiheit, jede Farbe beliebig oft benutzen zu können oder nicht, es also auch einfarbige Würfel geben darf. Wenn das nicht klar ist, mal die Abb2 rechts ansehen! ;-)
Da aber jeder Mensch Würfel als eigentlich gleich gefärbt betrachtet, wenn sie sich nur durch Drehung voneinander unterscheiden, sind es eigentlich viel weniger als 729. Da die Klassen in diesem Sinne gleicher Würfel aber unterschiedlich groß sind, lässt sich der Nachteil dieses kombinatorischen Ansatzes nicht so leicht heilen!
Eine Technik der Mathematik, solche Probleme zu lösen, ist die Klassifikation aller Würfel in Typen, die durch drehinvariante Eigenschaften beschrieben werden. Dazu ein einfaches Beispiel:
- Der Würfel Hans besteht aus einem Ring gelber Seitenflächen und zwei roten Deckeln.

- Der Würfel Oscar besteht aus einem blauen und einem gelben Hütchen.
Kein Mensch würde mehr versuchen nachzuprüfen, ob sich die beiden Würfel vielleicht durch Drehen in Deckung bringen lassen, denn Gelb-Rot bleibt auch nach dem Drehen Gelb-Rot und wird nicht etwa Blau-Gelb. Ring bleibt Ring. Hut bleibt Hut. Basta!
Aber so oder so: Wie viele Würfel gibt es nun eigentlich?
- Ein schönes Projekt für 2 - 3 Stunden.
- Arbeitsteilig zu bearbeiten in Gruppen.
- Unbedingt die obige Problematik mit den Schülern besprechen und schätzen lassen: "Wie viele sind nun von den 729 wirklich verschieden gefärbt?"
- Jede Gruppe berichtet von ihren Ergebnissen
- Dokumentiert auf einem kleinen Plakat und baut die Würfeltypen mit POLYDRON
- Am Ende liegt ein Baumdiagramm auf dem Boden mit den Ergebnissen
- Die Einfarbigen und Zweifarbigen kann man als Tipp gemeinsam machen und dann die dreifarbigen selber entwicklen lassen
Lösungsskizze
- Die einfarbigen Würfel
- Die zweifarbigen Würfel
- Seitenflächenfarbenverteilung: 1|5
- Seitenflächenfarbenverteilung: 2|4
- Seitenflächenfarbenverteilung: 3|3
- Die dreifarbigen Würfel
- Seitenflächenfarbenverteilung: 4|1|1
- Seitenflächenfarbenverteilung: 3|2|1
- Seitenflächenfarbenverteilung: 2|2|2
Insgesamt also 48 + ?
Viel Spaß beim Denken!