CUBE.CODES: Buchstabe O: Unterschied zwischen den Versionen
| Zeile 21: | Zeile 21: | ||
Wir lassen in unserer Galerie also nur Farbvarianten zu, die wirklich am Würfel zur Kontrolle hergezeigt wurden. | Wir lassen in unserer Galerie also nur Farbvarianten zu, die wirklich am Würfel zur Kontrolle hergezeigt wurden. | ||
| − | [https://de.wikipedia.org/wiki/Fixpunktfreie_Permutation Man kann übrigens zeigen, dass es 265 | + | [https://de.wikipedia.org/wiki/Fixpunktfreie_Permutation Man kann übrigens zeigen, dass es insgesamt 265 Farbvarianten vom Punktmuster gibt.] Aber welche davon kommen am RUBIK-Würfel nun wirklich vor? |
<br style="clear:left; "> | <br style="clear:left; "> | ||
Version vom 8. Dezember 2021, 09:19 Uhr
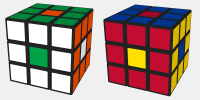
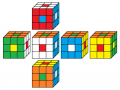
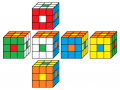
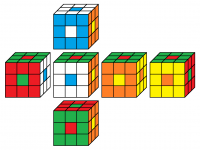
Das beliebteste Muster ist der Buchstabe O auf allen Seiten - anders ausgedrückt der Punkt auf allen Seiten. Du kannst ihn mit CUBE.CODES ganz einfach üben.
Mit der Forscherklasse 5_21/22 beschäftigen wir uns damit, wie viele Farbvarianten des Punktemusters es gibt ...
Unsere ersten Vermutungen sind nach etwas basteln: 36 | 37 | 33 | 30 | 50 | 49 | 32 | 60 , ... bin gespannt ;-)
Gallerie (noch unvollständig)
Mia, 5. Klasse
Ellie, 5. Klasse
Louisa, 5. Klasse
Ellie 2.0, 5. Klasse
Mia 2.0, 5. Klasse
Irreguläre Farbvarianten
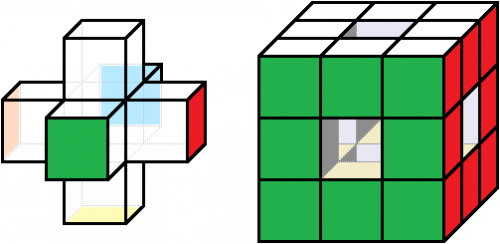
Die Sache ist komplizierter als man denkt! Man kann nämlich viele Farbkombinationen zeichnen, die aber (aus verschiedensten Gründen) nicht am RUBIK-Würfel vorkommen. Die abgebildete Variante zum Beispiel hat eine (unveränderliche) Farbfolge des Achsenkreuzes (der grüne Mittelpunktmüsste gegenüber dem blauen liegen). Außerdem gibt es ein grün-rot-oranges Eck nicht. Man müsste die Sticker vom Würfel abziehen und umkleben, um die Variante zu erhalten! ...
Wir lassen in unserer Galerie also nur Farbvarianten zu, die wirklich am Würfel zur Kontrolle hergezeigt wurden.
Man kann übrigens zeigen, dass es insgesamt 265 Farbvarianten vom Punktmuster gibt. Aber welche davon kommen am RUBIK-Würfel nun wirklich vor?
Idee zum systematischen Abzählen
Der Würfel besteht beim Punktemuster O aus zwei Teilen, die starr sind, also nicht verändert werden können: 1. Das Kreuz der Mittelpunkte, 2. Der Ring der 6 Ringe auf den Seiten, denn die Ecken bestimmen genau, welche Kanten benachbart sein müssen.
Die einzige Freiheit ist, den Ring abzunehmen, ihn irgendwie zu drehen und wieder aufzusetzen ... . Dabei dürfen allerdings kein Ring und Mittelpunkt, die aufeinander zum Liegen kommen, die gleiche Farbe haben!
Viel Möglichkeiten gibt's da ja nicht ...
Wie kann man also den rechten Ringring drehen?
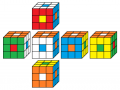
1. Weißer Ring oben ...
Keiner der Kombinationen ist eine Lösung, weil weiß immer auf weiß kommt!
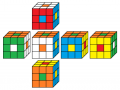
2. Grüner Ring oben ...
Die dritte Möglichkeit ist keine Lösung, weil rot auf rot kommt, der Rest geht!
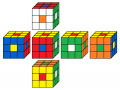
3. Roter Ring oben ...
Die zweite Möglichkeit ist keine Lösung, weil grün auf grün kommt, der Rest geht!
4. Blauer Ring oben ...
Die erste Möglichkeit ist keine Lösung, weil rot auf rot kommt, der Rest geht!
5. Oranger Ring oben ...
Die vierte Möglichkeit ist keine Lösung, weil grün auf grün kommt, der Rest geht!
6. Gelber Ring oben ...
Bei Möglichkeit eins kommen blau auf blau und grün auf grün.
Bei Möglichkeit drei kommen rot auf rot und orange auf orange. Beide sind keine Lösung, der Rest geht!
... ergibt 14 Lösungen!
