CUBE.CODES: Buchstabe O: Unterschied zwischen den Versionen
| Zeile 91: | Zeile 91: | ||
Datei: blau-orange.png | blau oben<br>orange vorne<br><span style="color: green; text-decoration: underline;"><b>6. Lösung</b></span><br>[https://ide.cube.codes/?init=loadFromUrl&url=https://share-repository.cube.codes/v1/appStates/4c8d4e82-2d6f-45df-bd2f-2e2b274962dd Beleg mit CUBE.CODES] | Datei: blau-orange.png | blau oben<br>orange vorne<br><span style="color: green; text-decoration: underline;"><b>6. Lösung</b></span><br>[https://ide.cube.codes/?init=loadFromUrl&url=https://share-repository.cube.codes/v1/appStates/4c8d4e82-2d6f-45df-bd2f-2e2b274962dd Beleg mit CUBE.CODES] | ||
</gallery><gallery> | </gallery><gallery> | ||
| − | Datei: orange-weiß.png | orange oben<br>weiß vorne<br><span style="color: green; text-decoration: underline;"><b>7. Lösung</b><br>Beleg mit CUBE.CODES | + | Datei: orange-weiß.png | orange oben<br>weiß vorne<br><span style="color: green; text-decoration: underline;"><b>7. Lösung</b></span><br>[https://ide.cube.codes/?init=loadFromUrl&url=https://share-repository.cube.codes/v1/appStates/3af34b2c-4065-407f-ac7f-1ecfc787a41d Beleg mit CUBE.CODES] |
Datei: orange-blau.png | orange oben<br>blau vorne<br><span style="color: red;">ungeklärt<br>Test mit CUBE.CODES</span> | Datei: orange-blau.png | orange oben<br>blau vorne<br><span style="color: red;">ungeklärt<br>Test mit CUBE.CODES</span> | ||
Datei: orange-gelb.png | orange oben<br>gelb vorne<br><span style="color: green; text-decoration: underline;"><b>8. Lösung</b><br>Beleg mit CUBE.CODES</span> | Datei: orange-gelb.png | orange oben<br>gelb vorne<br><span style="color: green; text-decoration: underline;"><b>8. Lösung</b><br>Beleg mit CUBE.CODES</span> | ||
Version vom 31. Mai 2022, 07:33 Uhr
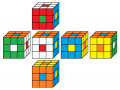
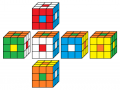
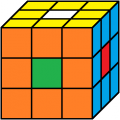
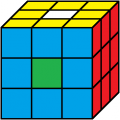
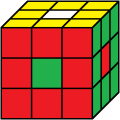
Das beliebteste Muster ist der Buchstabe O auf allen Seiten - anders ausgedrückt: Der Punkt auf allen Seiten.
Du kannst ihn mit CUBE.CODES ganz einfach üben.
Eine viel diskutierte Frage im Netz ist bei allen Mustern (so auch hier) immer wieder, welche Farbvarianten dabei möglich sind.
Farbvarianten, wenn man die Lösungen "malen" darf
Mit der Forscherklasse 5_21/22 beschäftigten wir uns damit, welche Farbvarianten man mit MS-paint "malen" kann. Unsere ersten Vermutungen (Umfrage mit Antworten aus dem Bauch raus) sind nach etwas basteln: 36 | 37 | 33 | 30 | 50 | 49 | 32 | 60 | 16, ... bin gespannt ;-). Nach einer kleinen MS-paint-Einweisung haben wir eine Form entwickelt, in der wir die Lösungen dokumentieren und die Würfel von allen Ansichten aus nachkontrollieren konnten:
irreguläre Farbvariante:
Ecke blau-weiß-grün gibt es nicht
irreguläre Farbvariante:
Die Mittelpunkte grün-blau sind nicht benachbart
Als immer mehr irreguläre "Gemälde" auftauchten (sie wären auch am Würfel möglich, wenn man die Sticker abziehen und umkleben würde), ließen wir Farbvarianten nur noch dann gelten, wenn man sie am Orginal-RUBIK-Würfel herzeigen konnte. Nach einigen Stunden wuchs dann die folgende Galerie, von der wir aber nicht wussten, ob sie vollständig ist:
Mia, 5. Klasse
Julia, 5. Klasse
Hannah, 5. Klasse
Louisa, 5. Klasse,
Mia, 5. Klasse,
Ellie, 5. Klasse
Jasmin, 5. Klasse,
Mia, 5. Klasse
Ellie, 5. Klasse,
Lina, 5. Klasse
Theresa, 5. Klasse,
Ellie, 5. Klasse
Mia, 5. Klasse
Wie viele Farbvarianten gibt es insgesamt?
Wir haben 6 Farben (1=weiß, 2=gelb, 3=grün, 4=blau, 5=rot, 6=orange). Eine Farbvariante (beim folgenden Beispiel Mias erste Lösung) könnte man so darstellen:
123456 (Mittelpunktsfarben)
652134 (Ringfarben)
Die 6 Ringe um die Mittelpunkte werden also vertauscht. Wenn zwei gleiche Zahlen untereinander stehen, entstehen einfarbige Flächen, also dürfen immer nur verschiedene Zahlen untereinander stehen. Merkt man sich die Bedeutung und Reihenfolge der Farben, würde es auch ausreichen nur die zweite Zeile zu notieren:
Mia: 652134
Notiert man alle Vertauschungen (Permutationen) von 6 Zahlen (wobei keine Zahlen an ihren originalen Positionen stehen dürfen), hätte man alle Farbvarianten. Ash aus der 9. Klasse hat im Netz die Info gefunden, dass es 265 Farbvarianten gibt!
- WIKIPEDIA-Artikel hierzu
- Da das Problem sog. fixpunktfreier Permutationen oft auftritt, gibt es dazu spannende mathematische Tricks. Eine nette andere Formulierung wäre: 6 Ehepaare gehen auf eine Party zum Tanzen. Beim ersten Tanz werden die Partner gelost. Jetzt kann sein, dass Ehepaare zusammen tanzen oder auch mal nur mit neuen Partnern. 265 von 720 möglichen Tanzpaarungen bringen nur neue Partner zusammen. Mehr im WIKIPEDIA-Artikel.
- Warum zum Teufel 265?
- Eine Antwort von Mathematikern findet Ihr im WIKIPEDIA-Artikel :-(
- Eine Antwort mit Schulmathematik
- Eine Antwort mit CUBE.CODES
- 295 ist aber noch nicht das Ende: Denn die 265 fixpunktfreien Permutationen notieren ja nur die verschiedenen Wände(sets) des Würfels, die es gibt. Man kann diese ja auch noch auf verschiedene Arten zusammensetzen. Spannendes Matheprojekt! ;-)
- Aber welche Farbvarianten kann man denn nun am RUBIK-Würfel wirklich verwirklichen?
Idee zum systematischen Abzählen
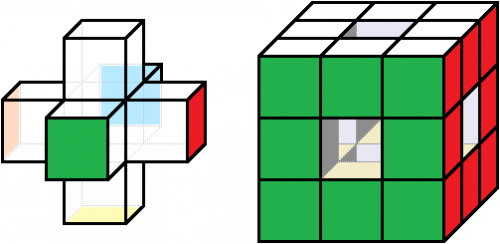
Die folgende Idee stellt sicher, dass nur Würfelchen verwendet werden, die es tatsächlich an einem orginal gefärbten Würfel gibt und dass das feste Achsenkreuz nicht missachtet wurde: Der Würfel besteht beim Punktemuster O aus zwei Teilen, die starr sind, also nicht verändert werden können: 1. Das Kreuz der Mittelpunkte, 2. Der Ring der 6 Ringe auf den Seiten, denn die Ecken bestimmen genau, welche Kanten benachbart sein müssen.
Die einzige Freiheit ist, den Ring wie einen Mantel abzunehmen, ihn irgendwie zu drehen und wieder anzuziehen ... . Dabei dürfen allerdings kein Ring und Mittelpunkt, die aufeinander zum Liegen kommen, die gleiche Farbe haben!
Viel Möglichkeiten gibt's da ja nicht ...
Wie kann man also den rechten Mantel drehen?
Sechs Möglichkeiten, welche Ringfarbe oben ist + jeweils vier Möglichkeiten, die Mäntel dann noch um die senkrechte Achse zu drehen ... :
Und welche Punktemuster kommen dabei raus beim Wiederaufsetzen?
weiß oben
grün vorne
alles einfarbig
weiß oben
rot vorne
weiß einfarbig
weiß oben
blau vorne
weiß einfarbig
weiß oben
orange vorne
weiß einfarbig
grün oben
weiß vorne
ungeklärt
Test mit CUBE.CODES
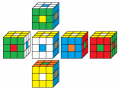
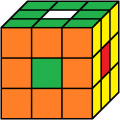
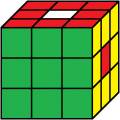
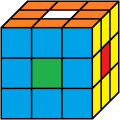
grün oben
orange vorne
1. Lösung
Beleg mit CUBE.CODES
grün oben
gelb vorne
rot einfarbig
grün oben
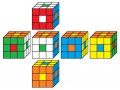
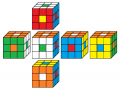
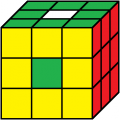
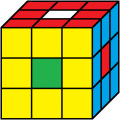
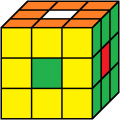
rot vorne
2. Lösung
Beleg mit CUBE.CODES
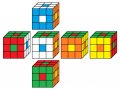
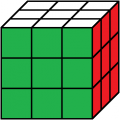
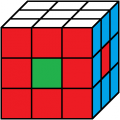
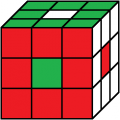
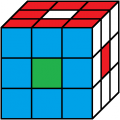
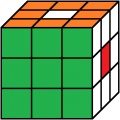
rot oben
weiß vorne
3. Lösung
Beleg mit CUBE.CODES
rot oben
grün vorne
grün einfarbig
rot oben
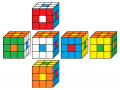
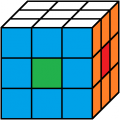
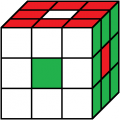
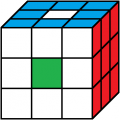
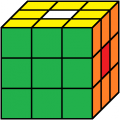
gelb vorne
4. Lösung
Beleg mit CUBE.CODES
rot oben
blau vorne
ungeklärt
Test mit CUBE.CODES
blau oben
weiß vorne
rot einfarbig
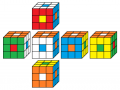
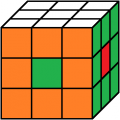
blau oben
rot vorne
5. Lösung
Beleg mit CUBE.CODES
blau oben
gelb vorne
ungeklärt
Test mit CUBE.CODES
blau oben
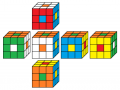
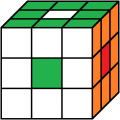
orange vorne
6. Lösung
Beleg mit CUBE.CODES
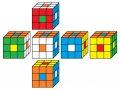
orange oben
weiß vorne
7. Lösung
Beleg mit CUBE.CODES
orange oben
blau vorne
ungeklärt
Test mit CUBE.CODES
orange oben
gelb vorne
8. Lösung
Beleg mit CUBE.CODES
orange oben
grün vorne
grün einfarbig
gelb oben
grün vorne
grün einfarbig
gelb oben
orange vorne
ungeklärt
Test mit CUBE.CODES
gelb oben
blau vorne
rot einfarbig
gelb oben
rot vorne
ungeklärt
Test mit CUBE.CODES
... ergibt 8 Lösungen! + 6 ungeklärte Bilder
