MML2021

Kann man Dummheit messen?

Das beliebte Spiel MEMORY wird gemeinhin als Gedächtnisspiel bezeichnet. Das ist nur zum Teil wahr!

In Wirklichkeit können wir natürlich unsere Gewinnchancen erheblich erhöhen, wenn wir aufgedeckte Karten gut merken können. Aber wir können uns auch strategisch geschickt oder ungeschickt verhalten. MEMORY ist also auch ein Strategiespiel. Und schließlich ist - wie bei fast allen Spielen - auch eine gehörige Portion Glück dabei. Also ist MEMORY irgendwie auch ein Glücksspiel.

Kann man nun die drei Anteile dieser Spielaspekte bestimmen?

• Wie viel ist Glück,
• Wie viel (taktisches) Können,
• Wie viel ist Gedächtnisleistung

... am Spielerfolg?

Einer meiner Professoren an der LMU München erstellte Gutachten für die Gerichte bei Streitigkeiten, ob ein Spiel (um Geld) nur eher ein Glücksspiel oder eher ein taktisch geprägtes Spiel ist.

Nun - ich will nicht streiten, aber mich interessiert einfach, wenn ich spiele (und z. B. 23 mal falsch aufdeckt habe), wie gut könnte ich sein, wenn ich keinen vermeidbaren Fehler machen würde!

Wie oft decke ich beim Spielen (im Schnitt) falsch auf, obwohl ich keinen Fehler gemacht hab?

Lasst uns mal spielen: >>> Memory mit der Vorlage Herbstbilder spielen

Meine Wartezeit auf den Sieg hängt also sehr entscheidend von der Spielsituation ab:

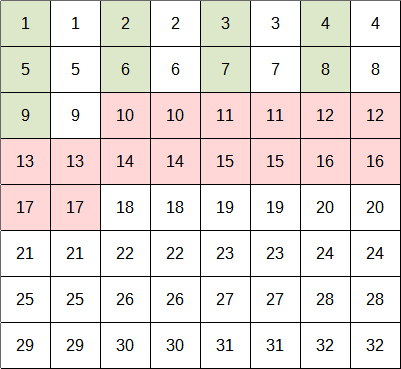
Es gibt immer Karten, die mich gar nicht interessieren (weiß), weil sie bereits erledigt sind oder ich sie schon kenne (obwohl ich sie wieder umdrehen musste). Interessant sind nur die farbigen Karten. Da gibt es die (rot), von denen noch beide unentdeckt sind und die (grün), deren Partnerkarte ich schon kenne.

Am besten, wir berechnen die Wartezeit für jede Spielsituation (n,m) (obwohl mich eigentlich nur (8,0) interessiert).

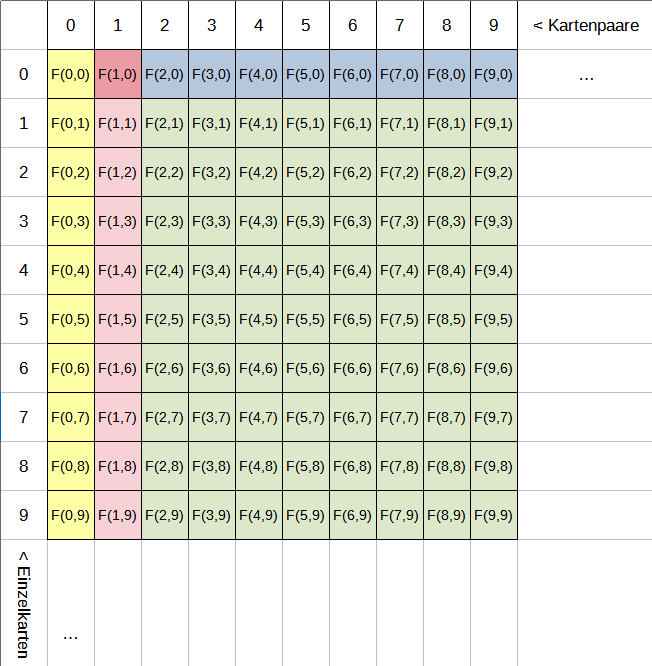
Mathematisch gesprochen möchte ich die Funktion F(n,m) berechnen (die durchschnittliche Anzahl Fehlaufdeckungen in einem Spiel bei optimalem Können), falls n Kartenpaare unentdeckt sind und mir noch m Karten unbekannt sind, deren Partner ich aber kenne!

Für F(0,0), F(0,1), F(0,2), ... ist die Antwort leicht:

Es gibt keine unbekannten Kartenpaare mehr. Ich decke einfach irgendeine unbekannte Einzelkarte auf und weiß immer den Partner. Ich werd also das Spiel immer mit 0 Fehler beenden.

Ebenso bei F(1,0)

Da gibt es nur ein Paar!

Wie sieht es mit F(1,m) aus, falls m>0?

F(1,1) = 2/3*1/2 + 1/3*0 = 1/3

F(1,m) = 2/(m+2)*m/(m+1)+m/(m+2)*F(1,m-1), also

F(1,2) = 2/4*2/3+2/4*1/3 = 1/2,

man kann also immer F(1,m) durch F(1,m-1) berechnen

Wie sieht es mit F(2,0) oder gar F(n,0) aus?

F(2,0) = 1/3*0 + 2/3*1 = 2/3

Für ein beliebiges n:

F(n,0) = 1/(2*n-1)*F(n-1,0)+(2*n-2)/(2*n-1)*(F(n-2,2)+1),

man kann also immer F(n,0) durch die F(n-1,0) und F(n-2,2) berechnen

Und schließlich die (grünen) F(n,m), mit m>1 und n>2

F(n,m) = 2*n/(2*n+m)*1/(2*n+m-1)*F(n-1,m)+2*n/(2*n+m)*(2*n-2)/(2*n+m-1)*(F(n-2,m+2)+1)+2*n/(2*n+m)*m/(2*n+m-1)*(F(n-1,m)+1)+m/(2*n+m)*F(n,m-1),

also durch F(n-1,m), F(n-2,m+2) und F(n,m-1) berechenbar

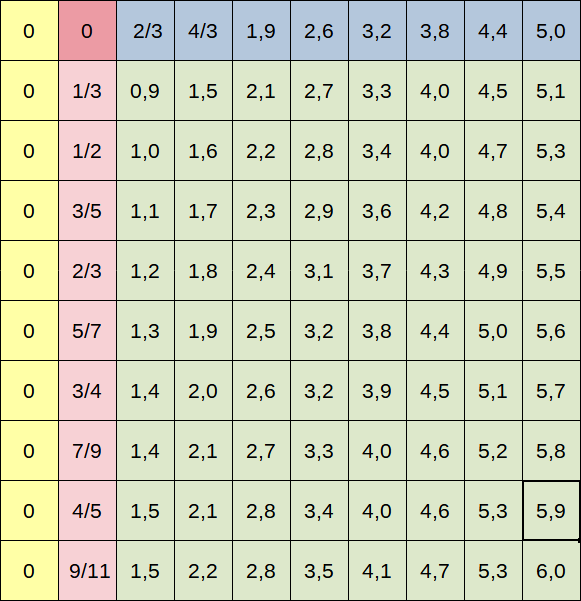
Insgesamt ergibt sich

Man kann sich mit den Formeln (iterativ) von Feld zu Feld hangeln und alle beliebigen Werte berechnen!

Man kann aber mit einer Programmiersprache (z.B. JavaScript) auch rekursiv vorgehen

function F(n,m) {
	if(n==0) return(0); else {
	if(n==1 && m==0) return(0); else {
	if(n==1 && m>0) return(2/(m+2)*m/(m+1)+m/(m+2)*F(1,m-1)); else {
	if(m==0) return(1/(2*n-1)*F(n-1,0)+(2*n-2)/(2*n-1)*(F(n-2,2)+1)); 
	else return(2*n/(2*n+m)*1/(2*n+m-1)*F(n-1,m)+2*n/(2*n+m)*(2*n-2)/(2*n+m-1)*(F(n-2,m+2)+1)+2*n/(2*n+m)*m/(2*n+m-1)*(F(n-1,m)+1)+m/(2*n+m)*F(n,m-1)); 
	}}}
}

UI.log(F(9,9));

>>> direkt zu CUBE.CODES