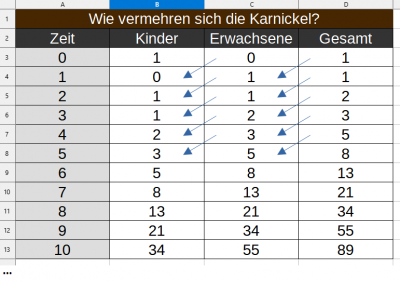
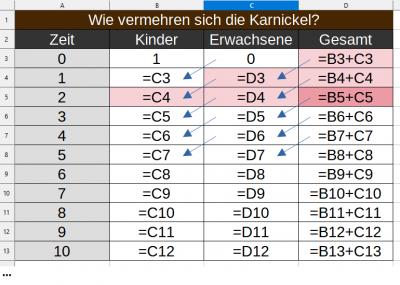
Wie vermehren sich die Karnickel? - in memoriam Fibonacci

exponentielles Wachstum

Lässt man einige Details weg, kann man sagen: Vermehrungen in der Natur vollziehen sich exponentiell! ... bedeutet z.B.

1 - 2 - 4 - 8 - 16 - 32 - 64 - ...

Annahme: Bekommt zum Beispiel ein Karnickel in einer Zeiteinheit im Schnitt einen Nachkommen, dann hat man (beginnend mit einem Karnickel)

• In der ersten Zeiteinheit (t=1) 1 Karnickel
• In der zweiten Zeiteinheit (t=2) 2 Karnickel (das eine, das zur Zeit t=1 schon lebte und das Neue)
• In der dritten Zeiteinheit (t=3) 4 Karnickel (die zwei, die zur Zeit (t=2) schon lebten und die von diesen auf die Welt gebrachten Neuen)
• In der vierten Zeiteinheit (t=4) 8 Karnickel (...)
• ...

In dieser einfachen Sicht werden viele (nicht sehr wichtige Details) weggelassen. Zum Beispiel brauchen Karnickel eine Zeit (das Warten auf die Geschlechtsreife), um selber wieder Kinder kriegen zu können. Bei Karnickel geht das ziemlich flott, in etwa in derselbe Zeit, in der ein Mutterkarnickel wieder die zweite Welle Kinder kriegen kann. Der Mathematiker Leonarda da Pisa, genannt: Fibonacci versuchte schon im tiefsten Mittelalter die exponentielle Sicht stärker zu verfeinern und versuchte zunächst das Warten auf die Geschlechtsreife zu berücksichtigen. Dabei kam er auf folgende Zahlenfolge: