Tag der Mathematik an der Staatlichen Realschule Bruckmühl, 17. März 2013, Würfel All Over

Seitenlänge = 3

Seitenlänge = 2

Seitenlänge = 1

>>> zurück zu den Lehrer:innenfortbildungen Mathematik und IT

Würfel

Würfel sind die einfachsten Körper, die wir in der Realschule kennen lernen. Im Lehrplan der 5. Klasse R6 begegnen uns die folgenden Fakten:

• Der Würfel hat 6 Seiten
• Der Würfel hat 8 Ecken
• Der Würfel hat 12 Kanten
• Die Oberfläche des Würfels hat Inhalt $$6a^2$$
• Der Rauminhalt des Würfels hat den Wert $$a^3$$
• Wir bauen Würfel aus verschiedenen Abwicklungen (Netzen) auf

Hat der Würfel noch andere interessante Wesenszüge zu bieten?

Würfel färben und Polyeder basteln

Mit dem System POLYDRON bzw. FRAMEWORK (... zu beziehen über das Mathematikum in Gießen; sehr zu empfehlen!) lassen sich einfache Würfel in verschiedenen Farben bauen.

Bausatz POLYDRON

• 1: Einfache Steckbrief-Aufgaben:
  • 1a: Ich bin ein Würfel
    • ... und bin dreifarbig.
    • ... Ein blaues Quadrat berührt dabei alle drei roten Quadrate,
    • ... ein weiteres blaues Quadrat berührt nur zwei rote Quadrate,
    • ... ein gelbes Quadrat berührt nur ein blaues Quadrat.
  • 1b: Mein Körper besteht aus acht gleichseitigen Dreiecken,
    • ... dabei werden immer gelbe Dreiecke mit roten verbunden.
    • ... Es gibt vier gelbe Dreiecke
    • ... und es werden nur zwei Farben benutzt.

• 2: Schwieriger ist: Gibt es immer nur einen solchen Körper oder sogar mehrere?
  • 2a: Ich bin ein dreifarbiger Würfel und habe keine bunte Kante (eine bunte Kante ist das, was man von Grenzen politischer Karten gewohnt ist, nämlich eine Kante mit zwei verschiedenfarbigen Nachbarflächen)
  • 2b: Ich bin ein dreifarbiger Würfel und habe eine bunte Kante
  • 2c: Ich bin ein dreifarbiger Würfel und habe zwei bunte Kanten
  • u. s. w.

• 3: Forschungsprojekt für eine Mathe-Freizeit: Welche dreifarbigen Würfel (bzw. wie viele) gibt es denn insgesamt ???
  • Projektseite: Matheprojekt: Würfel färben 1*6

• 4: Schönes Färbeproblem der schärferen Sorte (Prof. Steinlein LMU)
  • Förderverein der LMU - Mathematik; folgen Sie dem Link >>> Zeitschrift >>> DOWNLOAD-Archiv >>> Nummer 20 (Aufgabe) und 21 (Verschärfung + Lösung)
  • Neue Info (2022): Der Förderverein wurde umbenannt und der Webauftritt neu gestaltet. Ich konnte die alten Ausgaben der Zeitschriften letztens nicht mehr finden
  • Dokumentation einer Mathematik-Freizeit, auf der das Problem mit Schülern gelöst wurde: Matheprojekt: Würfel färben 4*6

Platonische Körper

Würfel sind Mitglied einer sehr erlesenen Familien von Körpern, den Platonischen Körpern. Diese Platonischen Körper sind sozusagen das regelmäßigste, was es bei räumlichen Vielecken (Polyedern) gibt.

• Sie bestehen aus lauter gleichen regelmäßigen Vielecken
• Es gibt einen Mittelpunkt, von dem sind ...
  • alle Flächen gleich weit weg,
  • alle Kanten (in Gestalt der Mittelpunkte) gleich weit weg und
  • alle Ecken gleich weit weg.

Mehr unter ...

• Platonische Körper bei WIKI

Warum gibt es nur diese 5 Platonischen Körper?

Beweis: Mit POLYDRON alle möglichen Hütchen an den Ecken ausprobieren ...

• gleichseitige Dreiecke ...
  • 3 an einem Eck >>> Tertraeder
  • 4 an einem Eck >>> Oktaeder
  • 5 an einem Eck >>> Ikosaeder
  • 6 an einem Eck >>> Fläche ist ausgefüllt, denn 6 mal 60 Grad ist 360 Grad, also keine Wölbung
  • 7 an einem Eck haben nicht Platz, mehr erst recht nicht
• Quadrate ...
  • 3 an einem Eck >>> Würfel (Hexaeder)
  • 4 an einem Eck >>> Fläche ist ausgefüllt, denn 4 mal 90 Grad ist 360 Grad, also keine Wölbung
  • 5 an einem Eck haben nicht Platz, mehr erst recht nicht
• regelmäßige Fünfecke ...
  • 3 an einem Eck >>> Dodekaeder
  • 4 an einem Eck >>> haben nicht Platz, weil 108 Grad mal 4 > 360 Grad, mehr erst recht nicht
• regelmäßege Sechsecke ...
  • 3 >>> Fläche ist ausgefüllt, denn 3 mal 120 Grad ist 360 Grad, also keine Wölbung
  • 4 an einem Eck haben nicht Platz, mehr erst recht nicht

Eulersche Polyederformel

Wie viele Ecken, Kanten und Flächen haben die Platonischen Körper?

Ergebnisse in: Tabelle in WIKI

Ist es Zufall oder eine Eigenschaft der Platonischen Körper, dass der Term

E=Ecken + Flächen - Kanten 

immer das Ergebnis 2 liefert? Teste mit anderen Polyedern!

Scheint für alle Körper zu stimmen!!! (Eulerscher Polyedersatz)

Eulersche Wege

Seitennachbarschaften

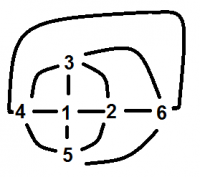
Der Würfel hat interessante Nachbarschaftseigenschaften:

• Die Nachbarschaften der Seiten (Jede Seite hat alle bis auf eine Seite als Nachbarn)
• Die Nachbarschaften der Ecken sieht man am Würfelkantengitter (Jede Ecke hat nur drei Nachbarn, Nachbarn sind 1, 2 oder gar 3 Kanten entfernt)

Dieses topologische Wesen des Würfels hat einige Konsequenzen:

• Man kann so von Fläche zu Fläche wandern (über die gemeinsame Grenze), dass man jede Fläche nur einmal besucht und letztlich alle einmal besucht hat.
• Versuchen Sie dies mit den Ecken (Dabei sind die Kanten die Wege!)

>>> Jahresbericht (Cappucino-Beweis)

Aufgabe: Wie sieht dies mit den anderen Platonischen Körpern aus?

RUMIS - Würfelvolumen und Teilbarkeit

Das Spiel RUMIS bietet interessante Lernumgebungen zu Würfelvolumen und Teilbarkeit: Projektseite: RUMIS

Ergänzung: Würde man bei einem Farbsatz (40 Elementar-Würfelchen) 13 Würfelchen weglassen, dann hätte man die Kubikzahl 27 und könnte einen Würfel bauen!

Piet Hein entdeckte (gelangweilt in einer Vorlesung von Heisenberg), dass es unter den RUMIS-Bausteinen 4 gibt, die besonders sind und genau Volumen 13 haben! Es sind genau die Teile, die keinen Knick haben, die sog. regulären Körper. Der SOMA-Würfel war geboren: Mit den irregulären Teilen eine RUMIS-Satzes könnte man also einen Würfel bauen - zumindest was das Volumen angeht!

Viel Spaß dabei!

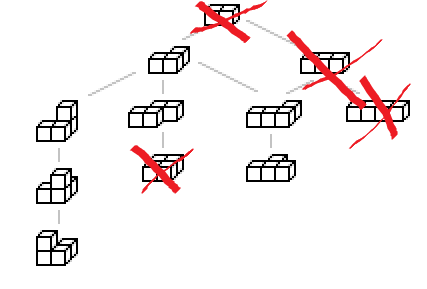
Wartezeiten beim Wandern auf einem Würfel

Ein Marienkäfer wandert auf den Kanten eines Würfel hin und her. An jeder Ecke dreht er ein paar mal und sucht dann (willkürlich) eine Kante für seinen Weiterweg aus. Wie viele Kanten braucht er im Schnitt, um an sein Ziel zu kommen?

Das Spiel SET

Das Spiel SET

Das Spiel SET in WIKI

• Die Karten eines SET-Spiels mit 3 Eigenschaften lassen sich auf einem Würfel anordnen.
  • Die SETs sind dann alle Geraden
    • Kanten sind die SETS, an denen sich eine Eigenschaft ändert
    • Die Flächendiagonalen die, an denen sich zwei Eigenschaften ändern
    • Die Raumdiagonalen sind die, an denen sich drei Eigenschaften ändern
    • Es gibt angeblich 9 Karten ohne ein SET, aber keine 10.
• Die Karten des Orginalsets lassen sich auf einem 4-dimensionalen Würfel anordnen
  • Die Sets sind ebenfalls alle Geraden
  • Die Maximalzahl an Karten ohne ein SET ist angeblich 20.

>>> Link: ... zu einer etwas anstrengenden aber sehr wahre und vollständigen Videostrecke zum Thema :-)

Quelle: http://behrenhoff.de/set/

Wolf-Ziege-Kohlkopf (Skizze)

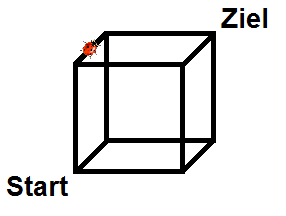
Ähnlich wie beim SET-Spiel lassen sich die Situationen beim Wolf-Ziege-Kohlkopf-Spiel auf einem Würfel anordnen. Die Punkte (x1, x2, x3), wobei xi = 0 oder 1 sein kann, geben dabei die Figuren an, die bereits im Ziel sind:

• x1 = 1 bedeutet Wolf im Ziel, x1 = 0, bedeutet Wolf nicht im Ziel
• x2 = 1 bedeutet Ziege im Ziel, ....
• x3 = 1 bedeutet Kohlkopf im Ziel, ....

Der Würfel ist ein Koordinatensystem. Der Start ist der Ursprung. Ziel ist (1,1,1). Die 8 Ecken des Würfels sind dann die 8 möglichen Spiel-Konstellationen.

Die 12 Kanten des Würfels sind die möglichen Übergänge von einer Konstellation zur anderen, denn zwei durch eine Kante verbundene Ecken, unterscheiden sich nur durch den Aufenthaltsort einer Figur, was der Bauer durch die Fahrt mit einer Figur überführen kann.

Lösung: Streiche alle die Kanten, die zu einer Fress-Situation führen. Der verbleibende Graph verbindet Start (0,0,0) und Ziel (1,1,1). Also ist eine Lösung möglich. Lösungen sind einfach alle Wege vom Start zum Ziel auf den nicht gestrichenen Kanten.