Lehrer:innenfortbildungen Mathematik und IT

Schon im R6-Lehrplan der 5. und 6. Klasse findet sich in Form der Baumdiagramme ein Graph (im Sinne der Graphentheorie), d.h. ein Konstrukt aus Knotenpunkten und (Verbindungs-)Strichen. Er dient dort als Hilfe zum systematischen Darstellen von Fallunterscheidungen, also zum systematischen Abzählen und in der 6. Klasse zum Bearbeiten zweistufiger Zufallsexperimente.
Baumdiagramme sind dabei immer unidirektional, d.h. man geht immer in eine Richtung und kehrt nie zu einem bereits besuchten Knotenpunkt zurück. Aber schon bei dem Versuch, die Möglichkeiten der Wege durch einen Irrgarten abzuzählen, kann man auf einmal wieder an einen Ort kommen, an dem man schon einmal war. Wie handhabt man solche (zyklischen) Graphen in der Schule? Wie mächtig das Instrument der Graphen (auch der zyklischen) ist, um vielfältige Probleme zu lösen, wie wertvoll sie als Veranschaulichung von Lernplanthemen sind und wie beziehungsreich sie besonders bei projektorientierten Mathematikstunden, -tagen oder gar wochen sind, soll dieser Workshop zeigen. Die Technik der Graphen erfüllt damit besonders die Forderung der SINUS-Initiative nach Visualisierung im Mathematikunterricht.
Besonders an MINT-Schulen werden Mathematische Projektstunden, -tage oder gar -wochen nachgefragt. Sie sind organisatorische Rahmenbedingungen, die einen erkenntnisorientierten Mathematikunterricht fördern können (Gedanken hierzu: "Eine Wortmeldung der Königsdisziplin"). Veränderte organisatorische Rahmen erfordern allerdings auch dazu passende Themen und Aufgaben (wie sie unsere Lehrbücher selten boeten), sprich: passende Mathematische Lernumgebungen. Ausführliche Gedanken hierzu will die folgende Studienarbeit anstoßen:
(2013), W. Lentner, "Mathematische Lernumgebungen für Projekttage"
Motivierender und nachhaltiger als ein Eigenstudium sind allerdings mathematische Tage mit ihrer ganzen Fachschaft an der Schule.
Inhaltsverzeichnis
Erstes Beispiel: Die Spiele RUMIS, SOMA und TETRIS (Klasse 5 oder 6)
Viele strategische Spiele benutzen aus Würfelchen zusammengesetzte Teile:
- Zum bekannten SOMA-Würfel gibt es Unmengen von Lernanregungen schon für die Grundschule.
- Weniger bekannt ist das vielfach prämierte Spiel RUMIS. Es eignet sich hervorragend für längere Projekte zu den Themen: Primfaktorzerlegung, Volumen von Würfel und Quader und Baumdiagramm.
- Alle Kinder kennen auch die zweidimensionale Version TETRIS.
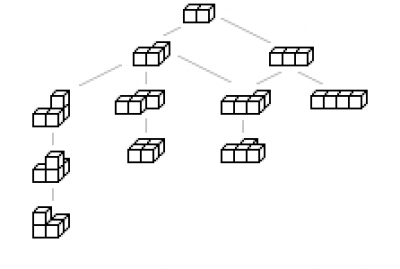
Sowohl beim Ermitteln aller möglichen Bauteile taucht das Baumdiagram auf (s. Abb. 1), als auch bei Fragen "Kann man alle Teile in Würfel oder Quader verbauen?" (Abb. 2). Ein interessantes Ergebnis: Der SOMA-Würfel benutzt nur einen Teil aller möglichen Teile (alle irregulären!). Mit allen Teilen könnte man keinen Würfel bauen!
Weiterführende Materialien:
- Projektseite: RUMIS
- http://www.bambusspiele.de/spiele/z_murmel/rumis.htm
- http://www.mathematische-basteleien.de/somawuerfel.htm
- //www.bildung-lsa.de/files/ffccd0c9c52d711b26f4972c31817cf6/Spiele_mit_dem_Somaw%C3%BCrfel.pdf]
- //de.wikipedia.org/wiki/Somaw%C3%BCrfel
- //www.friedrich-verlag.de/go/index.cfm?4B04A4AA60B943C281EB46A7C82F9981
Komplexer: Würfelfärbungen zählen
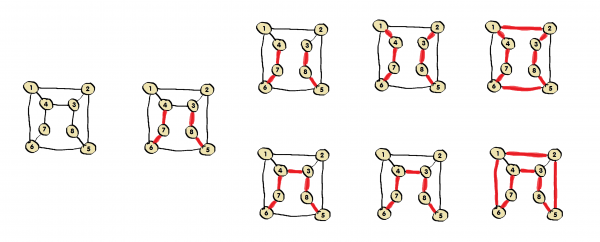
Wesentlich komplexer ist es, alle Würfelfärbungen eines berühmten Problems zu ermitteln (Abb. 3: Würfel färben 6*4). Davon gibt es viele einfachere Variationen (z.B.: Würfel färben 6*1).
Ein Beispiel mit Wahrscheinlichkeiten
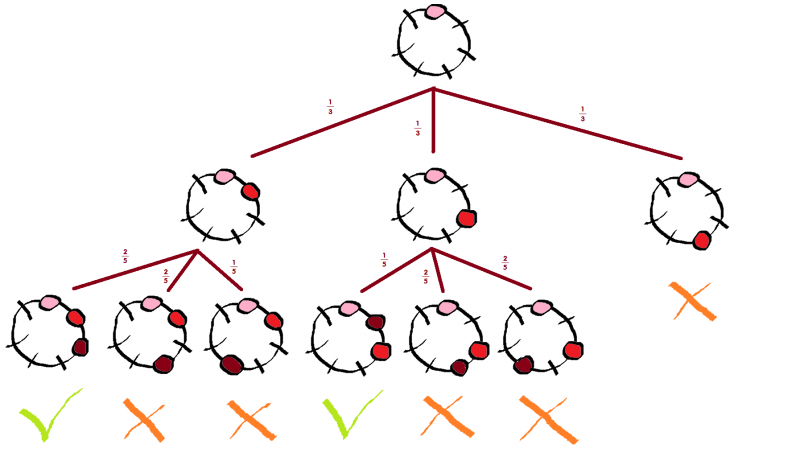
Beim bekannten Gesellschaftsspiel Mafia (alias Werwolf) tauchte auf einer Mathe-Freizeit einmal die Frage auf: "Können ausgeloste drei (böse) Spieler unter (insgesamt) 7 Spielern im Kreis zufällig genau nebeneinander sitzen?"
Dies kommt in: $\frac{1}{3} \cdot \frac{2}{5} + \frac{1}{3} \cdot \frac{1}{5} = \frac{3}{15} = \frac{1}{5} = 20$% aller Fälle vor, ist also gar nicht so selten!
Zyklische Graphen
Straßennetze sind typische Beispiele, bei denen ein Wege-Suchender Möglichkeiten hat, abzuzweigen (wie beim Baumdiagramm), aber zu einem bereits besuchten Ort zurückkommen kann.
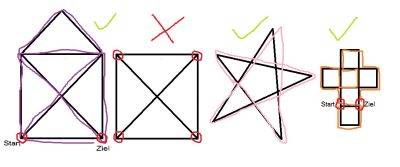
Königsberger Brückenproblem und andere Eulersche Wege
"Was ist die kürzeste Art, alle Straßen zu benutzen?"
- Erläuterungen zu den Eulerschen Wegen (Jahresbericht 2011/2012 der Mädchenrealschule Rosenheim
- Aufgabe 1 zu Eulerschen Wegen in einer Schulaufgabe 7aI
- Aufgabe 2 zu Eulerschen Wegen in einer Schulaufgabe 7aI
- Aufgabe 3 zu Eulerschen Wegen in einer Schulaufgabe 7aI
- Aufgabe 4 zu Eulerschen Wegen in einer Schulaufgabe 7aI
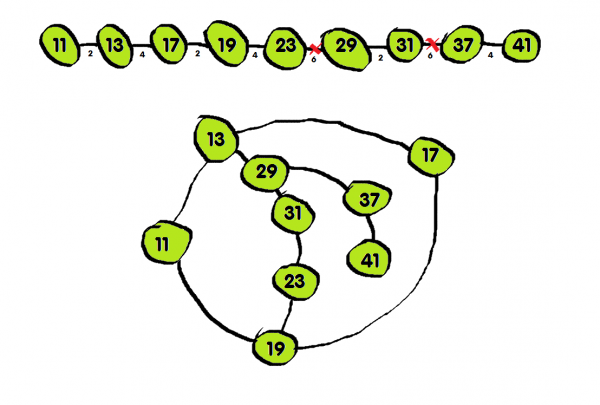
Das Problem des Handlungsreisenden - Hamilton-Wege
"Was ist die kürzeste Art, alle Orte zu besuchen?"
- Mit Geo-Brettern experimentieren (Das Problem ist mathematisch noch ungelöst!).
Minimale Spannbäume - Günstigste Verkabelungen
"Was ist die kürzeste Art, Orte zu verkabeln?"
- Wie oben ist das Problem ungelöst und kann nur durch Probieren gelöst werden, dabei werden beim Vergleich zweier Lösungen geometrische Grunderfahrungen gemacht: "Welche Lösung ist besser?", "warum?", "schräg ist länger als grade!", "Dreiecksungleichung!"
- Pythagoras für 5. Klässler
Weitere Spiele
- Die Türme von Hanoi
- Bauer - Ziege - Kohlkopf s. Tag der Mathematik, RS Bruckmühl
- SET s. Tag der Mathematik, RS Bruckmühl
Wartezeiten berechnen
"Wie lange braucht ein planloser Wanderer im Mittel, bis er in einem Wegenetz am Ziel ist?"
- Marienkäfer auf Würfelkanten
- Marienkäfer auf Tetraederkanten
>>> lineare Gleichungssysteme