Lehrer:innenfortbildungen Mathematik und IT: Unterschied zwischen den Versionen

Aus MINT.lentner.net
Zur Navigation springen Zur Suche springen
(Die Seite wurde neu angelegt: „ miniatur|400px|Abb. 1: Alle Teile des Spiels RUMIS; vgl. Tetris oder Soma-Würfel Datei: 11x2+1x3+1x5.png | thumb | Abb. 2: Kann man…“)
 
 
(23 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
−
[[Datei:Alleteile.png| miniatur|400px|Abb. 1: Alle Teile des Spiels RUMIS; vgl. Tetris oder Soma-Würfel]]
+
=== MINT-Fortbildung an der Staatlichen Realschule Bruckmühl, 26. Oktober 2022, Tetris, Soma, Rumis & Co ===
−
[[Datei: 11x2+1x3+1x5.png | thumb | Abb. 2: Kann man alle 6 Farbsätze verbauen? ($240=5^3+3^3+11\cdot 2^3$) | 400px]]
+
[[Datei: 14x2+2x4.png |thumb|links|250px|Eine der vielen Würfelfamilien unter den Lösungen]]
−
[[Datei: baum13.jpg | thumb | 400px | Abb. 3: Das fertige Baumdiagramm aller Wüfelfärbungen "[[Würfel färben 6*4]]" mit allen 3D-Würfeln aus der Gallerie!]]
 
  
 +
Tetris, Soma, Rumis & Co sind allesamt Spiele, die mit 2D- oder 3D-Polywürfeln mathematische Packungsprobleme behandeln. Sie fordern alle drei Lehrplanthemen der 5. Klasse (Mathematik) und schulen durch die Kombination aus natürlicher, spielerischer Motivation und haptischem Fordern die Entwicklung von kombinatorischem Denken und räumlichem Vorstellungsvermögen.<p>
 +
'''Lehrplanthemen:'''<br>
 +
- systematisches Abzählen (Baumdiagramm)<br>
 +
- Volumenrechnung mit Quadern und Polywürfeln (auch zeichnen)<br>
 +
- Teilbarkeit, Primfaktorzerlegung<p>
 +
>>> [[MINT-Fortbildung an der Staatlichen Realschule Bruckmühl, 26. Oktober 2022, Tetris, Soma, Rumis & Co | Zu den Fortbildungdokus ...]]<br>
 +
Die Fortbildungsunterlagen sind stark zusammenfassend und eher nur für Leher als Zielgruppe gedacht.
 +
<br style="clear:left; ">
  
−
Schon im '''R6-Lehrplan der 5. und 6. Klasse''' findet sich in Form der '''Baumdiagramme''' ein '''Graph (im Sinne der Graphentheorie'''), d.h. ein Konstrukt aus '''Knotenpunkten''' und (Verbindungs-)'''Strichen'''. Er dient dort als Hilfe zum systematischen Darstellen von Fallunterscheidungen, also zum systematischen Abzählen und in der 6. Klasse zum Bearbeiten '''zweistufiger Zufallsexperimente'''.  
+
=== MINT-Fortbildung an der Staatlichen Realschule Bruckmühl, 26. Oktober 2022, Mit PIVOT-Stickfigure-Manager digitale Daumenkinos erstellen ===
 +
[[Datei: pivot2.png |thumb|links|250px|PIVOT Animator]]
  
−
Baumdiagramme sind dabei immer '''unidirektional''', d.h. man geht immer in eine Richtung und kehrt nie zu einem bereits besuchten Knotenpunkt zurück. Aber schon bei dem Versuch, die Möglichkeiten der Wege durch einen Irrgarten abzuzählen, kann man auf einmal wieder an einen Ort kommen, an dem man schon einmal war. Wie handhabt man solche ('''zyklischen''') Graphen in der Schule? Wie '''mächtig das Instrument der Graphen''' (auch der zyklischen) ist, um vielfältige Probleme zu lösen, wie wertvoll sie als '''Veranschaulichung von Lernplanthemen''' sind und wie beziehungsreich sie besonders bei projektorientierten Mathematikstunden, -tagen oder gar wochen sind, soll dieser Workshop zeigen. Die Technik der Graphen erfüllt damit besonders die '''Forderung der SINUS-Initiative nach Visualisierung im Mathematikunterricht'''.
+
Im Modul IT 2.8.2 des Lehrplans IT PLUS erstellen wir mit Schüler:innen u.a. digitale Daumenkinos. Verteilt man die beiden Inhalte "pixelorientierte Techniken" und "objektorientierte Techniken" in etwa gleich auf die zur Verfügung stehenden 14 Wochenstunden und berücksichtigt evtl. Leistungserhebungen, dann bleiben Möglichkeiten übrig, die professionelle Programme völlig ausschließen. Der '''PIVOT Animator''' in seiner orginalen Version 2.2.7 trifft da genau das passende Niveau!
  
−
Besonders an MINT-Schulen werden '''Mathematische Projektstunden''', -tage oder gar -wochen nachgefragt. Sie sind organisatorische Rahmenbedingungen, die einen '''erkenntnisorientierten Mathematikunterricht''' fördern können (Gedanken hierzu: [[Medium:Wortmeldung.pdf|"Eine Wortmeldung der Königsdisziplin"]]). Veränderte organisatorische Rahmen erfordern allerdings auch dazu passende Themen und Aufgaben (wie sie unsere Lehrbücher selten boeten), sprich: passende '''Mathematische Lernumgebungen'''. Ausführliche Gedanken hierzu will die folgende Studienarbeit anstoßen:
+
>>> [[IT 2.8.2 Computeranimation (ca. 14 Std.) | Zu den Fortbildungsdokus ...]]
 +
<br style="clear:left; ">
  
−
(2013), W. Lentner, "Mathematische Lernumgebungen für Projekttage"
+
=== MINT-Fortbildung an der Johann-Rieder-RS Rosenheim, 8. März 2017, Das Geobrett von der 5. bis zur 9. Klasse===
−
* [[Medium:HausarbeitTitel.pdf|Titelseite und Inhaltsverzeichnis Hausarbeit]]
+
[[Datei: geobrett.png |thumb|links|250px|Aufgaben Geobrett]]
−
* [[Medium:HausarbeitVolltext.pdf|Volltext Hausarbeit]]
 
  
−
Motivierender und nachhaltiger als ein Eigenstudium sind allerdings '''mathematische Tage mit ihrer ganzen Fachschaft an der Schule'''.  
+
Schon im R6-Lehrplan Mathematik der 5. und 6. Klasse findet sich in Form der Baumdiagramme ein Graph (im Sinne der Graphentheorie), d.h. ein Konstrukt aus Knotenpunkten und (Verbindungs-)Strichen. Er dient in der R6 Bayern allerdings lediglich als Hilfe zum systematischen Darstellen von Fallunterscheidungen, also zum systematischen Abzählen und später zum Bearbeiten zweistufiger Zufallsexperimente. Die Anforderungen der bundesweiten Bildungsstandards reichen aber deutlich weiter, da Graphen schon alleine als '''Visualisierungsinstrument''' genial geeignet sind.
−
* [http://mrs-rosenheim.de/Flyer%20Mathematik%20im%20Projektunterricht.pdf Flyer Mathematik im Projektunterricht]
 
  
−
==Erstes Beispiel: Die Spiele RUMIS, SOMA und TETRIS (Klasse 5 oder 6)==
+
>>> [[Medium: geobrettscript.pdf | Es ist ein Handout der Fortbildung im pdf-Format verfügbar]]<br>
−
Viele strategische Spiele benutzen aus Würfelchen zusammengesetzte Teile:
+
>>> [[Medium: sageobrett.pdf | Schulaufgaben-Aufgabe aus dem Themengebiet (Spannbaum) im pdf-Format verfügbar]]<br>
−
* Zum bekannten '''SOMA-Würfel''' gibt es Unmengen von Lernanregungen schon für die Grundschule.
 
−
* Weniger bekannt ist '''das vielfach prämierte Spiel RUMIS'''. Es eignet sich hervorragend für längere Projekte zu den Themen: '''Primfaktorzerlegung, Volumen von Würfel und Quader und Baumdiagramm'''.
 
−
* Alle Kinder kennen auch die zweidimensionale Version '''TETRIS'''.
 
  
−
Sowohl beim Ermitteln aller möglichen Bauteile taucht das Baumdiagram auf (s. Abb. 1), als auch bei Fragen "Kann man alle Teile in Würfel oder Quader verbauen?" (Abb. 2). Ein interessantes Ergebnis: Der SOMA-Würfel benutzt nur einen Teil aller möglichen Teile (alle irregulären!). Mit allen Teilen könnte man keinen Würfel bauen!
+
<br style="clear:left; ">
  
−
Weiterführende Materialien:
+
=== MINT-Fortbildung an der Johann-Rieder-RS Rosenheim, 13. März 2016, Wie fallen die Würfel? NN===
−
* [[Projektseite: RUMIS]]
+
<br style="clear:left; ">
−
* [http://www.bambusspiele.de/spiele/z_murmel/rumis.htm http://www.bambusspiele.de/spiele/z_murmel/rumis.htm]
 
−
* [http://www.mathematische-basteleien.de/somawuerfel.htm http://www.mathematische-basteleien.de/somawuerfel.htm]
 
−
* [http://www.bildung-lsa.de/files/ffccd0c9c52d711b26f4972c31817cf6/Spiele_mit_dem_Somaw%C3%BCrfel.pdf //www.bildung-lsa.de/files/ffccd0c9c52d711b26f4972c31817cf6/Spiele_mit_dem_Somaw%C3%BCrfel.pdf]]
 
−
* [http://de.wikipedia.org/wiki/Somaw%C3%BCrfel //de.wikipedia.org/wiki/Somaw%C3%BCrfel]
 
−
* [http://www.friedrich-verlag.de/go/index.cfm?4B04A4AA60B943C281EB46A7C82F9981 //www.friedrich-verlag.de/go/index.cfm?4B04A4AA60B943C281EB46A7C82F9981]
 
  
−
==Komplexer: Würfelfärbungen zählen==
+
=== MINT-Fortbildung an der Johann-Rieder-RS Rosenheim, 5. März 2015, Visualisierung durch Graphen ===
−
Wesentlich komplexer ist es, alle Würfelfärbungen eines berühmten Problems zu ermitteln (Abb. 3: [[Würfel färben 6*4]]). Davon gibt es viele einfachere Variationen (z.B.: [[Würfel färben 6*1]]).
+
[[Datei: 2013.png |thumb|links|250px|Aufgabe 1 des Landeswettbewerbs Mathematik 2010 mit Graphen lösen]]
  
−
==Ein Beispiel mit Wahrscheinlichkeiten==
+
Schon im R6-Lehrplan Mathematik der 5. und 6. Klasse findet sich in Form der Baumdiagramme ein Graph (im Sinne der Graphentheorie), d.h. ein Konstrukt aus Knotenpunkten und (Verbindungs-)Strichen. Er dient in der R6 Bayern allerdings lediglich als Hilfe zum systematischen Darstellen von Fallunterscheidungen, also zum systematischen Abzählen und später zum Bearbeiten zweistufiger Zufallsexperimente. Die Anforderungen der bundesweiten Bildungsstandards reichen aber deutlich weiter, da Graphen schon alleine als '''Visualisierungsinstrument''' genial geeignet sind.
−
Beim bekannten Gesellschaftsspiel [http://www.mafiaspiel.de/ Mafia (alias Werwolf)] tauchte auf einer Mathe-Freizeit einmal die Frage auf: "Können ausgeloste drei (böse) Spieler unter (insgesamt) 7 Spielern im Kreis zufällig genau nebeneinander sitzen?"
 
  
−
[[Datei:mafiaproblem.png | 800px]]
+
>>> [[MINT-Fortbildung an der Johann-Rieder-RS Rosenheim, 5. März 2015, Visualisierung durch Graphen | Zu den Fortbildungsdokus ...]]
 +
<br style="clear:left; ">
  
−
Dies kommt in: $\frac{1}{3} \cdot \frac{2}{5} + \frac{1}{3} \cdot  \frac{1}{5} = \frac{3}{15} = \frac{1}{5} = 20$% aller Fälle vor, ist also gar nicht so selten!
+
===Tag der Mathematik an der Franz-von-Assisi-Realschule Freilassing, 25. März 2014, Erkenntnisorientierter Mathematikunterricht durch Handlungsorientierung NN ===
 +
<br style="clear:left; ">
  
−
==Zyklische Graphen==
+
=== MINT-Fortbildung an der Johann-Rieder-RS Rosenheim, 11. März 2014, Grundlagen mathematischer Projektstunden; POLYDRON ===
−
Straßennetze sind typische Beispiele, bei denen ein Wege-Suchender Möglichkeiten hat, abzuzweigen (wie beim Baumdiagramm), aber zu einem bereits besuchten Ort zurückkommen kann.
+
[[Datei: POLYDRON.jpg |thumb|links|250px|Baukasten Polydron]]
−
===Königsberger Brückenproblem und andere Eulersche Wege===
 
−
"Was ist die kürzeste Art, alle Straßen zu benutzen?"
 
−
[[Datei:Mintmathe2.jpg | thumb | 400px | Finde Eulersche Wege!]]
 
  
−
* [[Medium:MINT.pdf | Erläuterungen zu den Eulerschen Wegen (Jahresbericht 2011/2012 der Mädchenrealschule Rosenheim]]
+
Mathematische Projektstunden, -tage oder gar -wochen sind organisatorische Rahmenbedingungen, die einen '''erkenntnisorientierten Mathematikunterricht (EOM)''' fördern können (Gedanken hierzu: [[Medium:Wortmeldung.pdf|"Eine Wortmeldung der Königsdisziplin"]]). Veränderte organisatorische Rahmen erfordern allerdings auch dazu passende Themen und Aufgaben, sprich: passende Mathematische Lernumgebungen. Ausführliche Gedanken hierzu will die folgende Studienarbeit anstoßen:
−
* [[Medium:SAEuler1.pdf | Aufgabe 1 zu Eulerschen Wegen in einer Schulaufgabe 7aI]]
 
−
* [[Medium:SAEuler2.pdf | Aufgabe 2 zu Eulerschen Wegen in einer Schulaufgabe 7aI]]
 
−
* [[Medium:SAEuler3.pdf | Aufgabe 3 zu Eulerschen Wegen in einer Schulaufgabe 7aI]]
 
−
* [[Medium:SAEuler4.pdf | Aufgabe 4 zu Eulerschen Wegen in einer Schulaufgabe 7aI]]
 
  
−
===Das Problem des Handlungsreisenden - Hamilton-Wege===
+
(2013), W. Lentner, "Mathematische Lernumgebungen für Projekttage"<br>
−
"Was ist die kürzeste Art, alle Orte zu besuchen?"
+
>>> [[Medium:HausarbeitTitel.pdf|Titelseite und Inhaltsverzeichnis Hausarbeit]]<br>
 +
>>> [[Medium:HausarbeitVolltext.pdf|Volltext Hausarbeit]]
  
−
* Mit Geo-Brettern experimentieren (Das Problem ist mathematisch noch ungelöst!).
+
In den beiden Workshops der MINT-Fortbildung an der Johann-Rieder-RS, Rosenheim, werden einige Lernumgebungen vorgestellt, die am Lehrplan der 5. und 6. Klassen der bayerischen R6 anknüpfen:
  
−
===Minimale Spannbäume - Günstigste Verkabelungen===
+
>>> [[MINT-Fortbildung an der Johann-Rieder-RS Rosenheim, 11. März 2014, Grundlagen mathematischer Projektstunden; POLYDRON | Zu den Fortbildungsdokus ...]]
−
"Was ist die kürzeste Art, Orte zu verkabeln?"
+
<br style="clear:left; ">
  
−
* Wie oben ist das Problem ungelöst und kann nur durch Probieren gelöst werden, dabei werden beim Vergleich zweier Lösungen geometrische Grunderfahrungen gemacht: "Welche Lösung ist besser?", "warum?", "schräg ist länger als grade!", "Dreiecksungleichung!"
+
===Tag der Mathematik an der Staatlichen Realschule Bruckmühl, 17. März 2013, Würfel All Over ===
−
* Pythagoras für 5. Klässler
+
[[Datei: set1.jpg |thumb|links|250px|Was hat SET mit einem Würfel zu tun?]]
  
−
==Weitere Spiele==
+
'''Würfel sind die einfachsten Körper''', die wir in der Realschule kennen lernen. Im Lehrplan der 5. Klasse R6 begegnen uns die folgenden Fakten:<br>
−
* Die Türme von Hanoi
+
- Der Würfel hat 6 Seiten<br>
−
** [[Medium:Schulaufgabehanoi.pdf | Eine Schulaufgabe zu den Türmen von Hanoi]]
+
- Der Würfel hat 8 Ecken<br>
−
** [http://www.mrs-rosenheim.de/hanoi/2/index.html Projektseite (noch nicht vollständig)]
+
- Der Würfel hat 12 Kanten<br>
−
* Bauer - Ziege - Kohlkopf s. [[Tag der Mathematik, RS Bruckmühl]]
+
- Die Oberfläche des Würfels hat Inhalt $$6a^2$$<br>
−
* SET s. [[Tag der Mathematik, RS Bruckmühl]]
+
- Der Rauminhalt des Würfels hat den Wert $$a^3$$<br>
 +
- Wir bauen Würfel aus ''verschiedenen'' Abwicklungen (Netzen) auf<p>
  
−
==Wartezeiten berechnen==
+
Aber, ...<br>
−
"Wie lange braucht ein planloser Wanderer im Mittel, bis er in einem Wegenetz am Ziel ist?"
+
'''Hat der Würfel noch andere interessante Wesenszüge zu bieten?'''<p>
 +
>>> [[Tag der Mathematik an der Staatlichen Realschule Bruckmühl, 17. März 2013, Würfel All Over | Zu den Fortbildungdokus ...]]
 +
<br style="clear:left; ">
  
−
* Marienkäfer auf Würfelkanten
+
===MINT-Fortbildung an der Städtischen Realschule für Mädchen Rosenheim, 6. März 2013, Was ist guter Mathematikunterricht? NN ===
−
* Marienkäfer auf Tetraederkanten
+
<br style="clear:left; ">
  
−
>>> lineare Gleichungssysteme
+
===Tag der Mathematik an der Karl-Meichelbeck-Realschule Freising, 27. März 2012, Was ist guter Mathematikunterricht? NN ===
−
 
+
<br style="clear:left; ">
−
==Landeswettbewerb Mathematik==
 
−
=== [[Medium:LW2013.pdf | Aufgabe 1 - 2010: ]] ===
 
−
 
 
−
[[Datei:2013.png | 600px]]
 
−
 
 
−
=== [[Medium:LW2010.pdf | Aufgabe 1 - 2013:]] ===
 
−
 
 
−
[[Datei:2010.png | 600px]]
 

Aktuelle Version vom 30. Oktober 2022, 14:41 Uhr

MINT-Fortbildung an der Staatlichen Realschule Bruckmühl, 26. Oktober 2022, Tetris, Soma, Rumis & Co

Eine der vielen Würfelfamilien unter den Lösungen

Tetris, Soma, Rumis & Co sind allesamt Spiele, die mit 2D- oder 3D-Polywürfeln mathematische Packungsprobleme behandeln. Sie fordern alle drei Lehrplanthemen der 5. Klasse (Mathematik) und schulen durch die Kombination aus natürlicher, spielerischer Motivation und haptischem Fordern die Entwicklung von kombinatorischem Denken und räumlichem Vorstellungsvermögen.

Lehrplanthemen:
- systematisches Abzählen (Baumdiagramm)
- Volumenrechnung mit Quadern und Polywürfeln (auch zeichnen)
- Teilbarkeit, Primfaktorzerlegung

>>> Zu den Fortbildungdokus ...
Die Fortbildungsunterlagen sind stark zusammenfassend und eher nur für Leher als Zielgruppe gedacht.

MINT-Fortbildung an der Staatlichen Realschule Bruckmühl, 26. Oktober 2022, Mit PIVOT-Stickfigure-Manager digitale Daumenkinos erstellen

PIVOT Animator

Im Modul IT 2.8.2 des Lehrplans IT PLUS erstellen wir mit Schüler:innen u.a. digitale Daumenkinos. Verteilt man die beiden Inhalte "pixelorientierte Techniken" und "objektorientierte Techniken" in etwa gleich auf die zur Verfügung stehenden 14 Wochenstunden und berücksichtigt evtl. Leistungserhebungen, dann bleiben Möglichkeiten übrig, die professionelle Programme völlig ausschließen. Der PIVOT Animator in seiner orginalen Version 2.2.7 trifft da genau das passende Niveau!

>>> Zu den Fortbildungsdokus ...

MINT-Fortbildung an der Johann-Rieder-RS Rosenheim, 8. März 2017, Das Geobrett von der 5. bis zur 9. Klasse

Aufgaben Geobrett

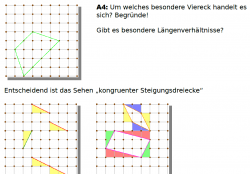
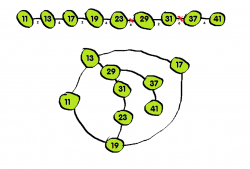
Schon im R6-Lehrplan Mathematik der 5. und 6. Klasse findet sich in Form der Baumdiagramme ein Graph (im Sinne der Graphentheorie), d.h. ein Konstrukt aus Knotenpunkten und (Verbindungs-)Strichen. Er dient in der R6 Bayern allerdings lediglich als Hilfe zum systematischen Darstellen von Fallunterscheidungen, also zum systematischen Abzählen und später zum Bearbeiten zweistufiger Zufallsexperimente. Die Anforderungen der bundesweiten Bildungsstandards reichen aber deutlich weiter, da Graphen schon alleine als Visualisierungsinstrument genial geeignet sind.

>>> Es ist ein Handout der Fortbildung im pdf-Format verfügbar
>>> Schulaufgaben-Aufgabe aus dem Themengebiet (Spannbaum) im pdf-Format verfügbar


MINT-Fortbildung an der Johann-Rieder-RS Rosenheim, 13. März 2016, Wie fallen die Würfel? NN


MINT-Fortbildung an der Johann-Rieder-RS Rosenheim, 5. März 2015, Visualisierung durch Graphen

Aufgabe 1 des Landeswettbewerbs Mathematik 2010 mit Graphen lösen

Schon im R6-Lehrplan Mathematik der 5. und 6. Klasse findet sich in Form der Baumdiagramme ein Graph (im Sinne der Graphentheorie), d.h. ein Konstrukt aus Knotenpunkten und (Verbindungs-)Strichen. Er dient in der R6 Bayern allerdings lediglich als Hilfe zum systematischen Darstellen von Fallunterscheidungen, also zum systematischen Abzählen und später zum Bearbeiten zweistufiger Zufallsexperimente. Die Anforderungen der bundesweiten Bildungsstandards reichen aber deutlich weiter, da Graphen schon alleine als Visualisierungsinstrument genial geeignet sind.

>>> Zu den Fortbildungsdokus ...

Tag der Mathematik an der Franz-von-Assisi-Realschule Freilassing, 25. März 2014, Erkenntnisorientierter Mathematikunterricht durch Handlungsorientierung NN


MINT-Fortbildung an der Johann-Rieder-RS Rosenheim, 11. März 2014, Grundlagen mathematischer Projektstunden; POLYDRON

Baukasten Polydron

Mathematische Projektstunden, -tage oder gar -wochen sind organisatorische Rahmenbedingungen, die einen erkenntnisorientierten Mathematikunterricht (EOM) fördern können (Gedanken hierzu: "Eine Wortmeldung der Königsdisziplin"). Veränderte organisatorische Rahmen erfordern allerdings auch dazu passende Themen und Aufgaben, sprich: passende Mathematische Lernumgebungen. Ausführliche Gedanken hierzu will die folgende Studienarbeit anstoßen:

(2013), W. Lentner, "Mathematische Lernumgebungen für Projekttage"
>>> Titelseite und Inhaltsverzeichnis Hausarbeit
>>> Volltext Hausarbeit

In den beiden Workshops der MINT-Fortbildung an der Johann-Rieder-RS, Rosenheim, werden einige Lernumgebungen vorgestellt, die am Lehrplan der 5. und 6. Klassen der bayerischen R6 anknüpfen:

>>> Zu den Fortbildungsdokus ...

Tag der Mathematik an der Staatlichen Realschule Bruckmühl, 17. März 2013, Würfel All Over

Was hat SET mit einem Würfel zu tun?

Würfel sind die einfachsten Körper, die wir in der Realschule kennen lernen. Im Lehrplan der 5. Klasse R6 begegnen uns die folgenden Fakten:
- Der Würfel hat 6 Seiten
- Der Würfel hat 8 Ecken
- Der Würfel hat 12 Kanten
- Die Oberfläche des Würfels hat Inhalt $$6a^2$$
- Der Rauminhalt des Würfels hat den Wert $$a^3$$

- Wir bauen Würfel aus verschiedenen Abwicklungen (Netzen) auf

Aber, ...
Hat der Würfel noch andere interessante Wesenszüge zu bieten?

>>> Zu den Fortbildungdokus ...

MINT-Fortbildung an der Städtischen Realschule für Mädchen Rosenheim, 6. März 2013, Was ist guter Mathematikunterricht? NN


Tag der Mathematik an der Karl-Meichelbeck-Realschule Freising, 27. März 2012, Was ist guter Mathematikunterricht? NN


Abgerufen von „http://mint.lentner.net/index.php?title=Lehrer:innenfortbildungen_Mathematik_und_IT&oldid=5920“