R6 Tabellenkalkulation - G Siedler von Catan: Unterschied zwischen den Versionen
| (48 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
Wir nutzen die Tabellenkalkulation zur '''Simulation''' eines Zufallsexperiments und damit zur Klärung einer ernsten Forschungsfrage. Die These vieler erfahrener Siedlerspieler lautet: '''Beim Schicksalswürfeln (mit 2 Würfeln) kommen Augensummen in der Mitte (..., 6, 7, 8, ...) häufiger vor als extreme Augensummen (2, 3, ..., 11, 12)'''. Mathefreaks wissen, ob das stimmt (durch sog. analytisches Denken). Wir wollen es einfach ausprobieren (die sog. empirische Methode)! | Wir nutzen die Tabellenkalkulation zur '''Simulation''' eines Zufallsexperiments und damit zur Klärung einer ernsten Forschungsfrage. Die These vieler erfahrener Siedlerspieler lautet: '''Beim Schicksalswürfeln (mit 2 Würfeln) kommen Augensummen in der Mitte (..., 6, 7, 8, ...) häufiger vor als extreme Augensummen (2, 3, ..., 11, 12)'''. Mathefreaks wissen, ob das stimmt (durch sog. analytisches Denken). Wir wollen es einfach ausprobieren (die sog. empirische Methode)! | ||
| − | '''Wir lernen:''' Erzeugen von '''Zufallszahlen''' und damit Datenreihen, die reale Vorgänge simulieren. Wir lassen den PC Würfeln. Wir lernen Datenreihen mit der Funktion '''ZÄHLENWENN''' auszuzählen. Die Funktion '''neu berechnen (F9)'''. Wir lernen Tricks zum Siedlerspielen, entdecken die '''Gaußsche Glockenkurve''', das '''Gesetz der großen Zahl''' und den ''' | + | '''Wir lernen:''' Erzeugen von '''Zufallszahlen''' und damit Datenreihen, die reale Vorgänge simulieren. Wir lassen den PC Würfeln. Wir lernen Datenreihen mit der Funktion '''ZÄHLENWENN''' auszuzählen. Die Funktion '''neu berechnen (F9)'''. Wir lernen Tricks zum Siedlerspielen, entdecken die '''Gaußsche Glockenkurve''', das '''Gesetz der großen Zahl''' und den '''Zentralen Grenzwertsatz'''! |
<br style="clear:left; "> | <br style="clear:left; "> | ||
| − | * [[Media: | + | * [[Media: tk12.ods | TK12: Siedler von Catan - 20x würfeln - Lösungsmuster]] |
| − | * [[Media: | + | * [[Media: tk13.ods | TK13: Siedler von Catan - 20x würfeln - Lösungsmuster perfekt formatiert]] |
| − | * [[Media: | + | * [[Media: tk14.ods | TK14: Siedler von Catan - 2000x würfeln - Das Gesetz der großen Zahl]] |
| − | * [[Media: | + | * [[Media: tk15.ods | TK15: Siedler von Catan - 2000x mit 5 Würfel würfeln - Der zentrale Grenzwertsatz]] |
===Aufgabe 1:=== | ===Aufgabe 1:=== | ||
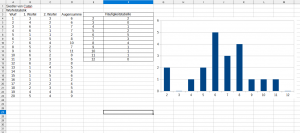
| − | + | [[Datei: siedler2.png |thumb|links|300px|Screenshot: Siedler von Catan Zufalls-Experiment]] | |
| − | + | '''Lass Calc den PC 20x zwei Würfel werfen''' und stelle übersichtlich die Ergebnisse dar.<br> | |
| − | + | '''Überlege:''' Stimmt die Vermutung, dass 'mittlere Augensummen häufiger' vorkommen?<br> | |
| − | + | '''Drücke <F9>''' und lass den PC mehrmals würfeln. Was stellst Du fest? | |
| − | + | * [[Media: tk12.ods | TK12: Siedler von Catan - 20x würfeln - Lösungsmuster]] | |
| − | + | <br style="clear:left; "> | |
| − | |||
| − | |||
| − | |||
| − | * [[Media: | ||
===Aufgabe 2:=== | ===Aufgabe 2:=== | ||
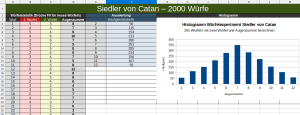
| − | + | [[Datei: siedler1.png |thumb|links|300px|Musterlösung formatiert]] | |
| − | * [[Media: | + | Formatiere Deine Statistik sauber, anschaulich und übersichtlich - '''form follows function ;-)'''. Achte auf folgende Punkte: |
| + | * Gliedernde Infos dominant - Ähnliches ähnlich - Verschiedenes verschieden ... | ||
| + | * Die Skala auf der y-Achse soll nicht immer '''hüpfen'''! | ||
| + | * [[Media: tk13.ods | TK13: Siedler von Catan - 20x würfeln - Lösungsmuster perfekt formatiert]] | ||
| + | <br style="clear:left; "> | ||
===Aufgabe 3:=== | ===Aufgabe 3:=== | ||
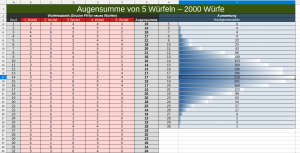
| − | + | [[Datei: siedler3.png |thumb|links|300px|Siedler von Catan 2000x würfeln]] | |
| − | * [[Media: | + | Würfelt man nur 20x, dann ist kaum etwas Besonderes erkennbar. Vor allem ist es sehr stark vom Zufall abhängig (auch sonst im Leben kommen ja seltene Dinge vor - aber eben selten). Man kann also aus dem Vorkommen (bei 20x) nicht die Häufigkeit '''auf Dauer schließen'''. Seltene Ereignisse können sogar häufig vorkommen, aber es kommt eben selten vor, dass seltene Ereignisse häufig vorkommen. Was tun?! <br> |
| + | *'''TIPP:''' Oft <F9> drücken und '''Erfahrung aufsammeln''' - wie erfahrene Spieler >>> Aufgabe 1! | ||
| + | *'''TIPP:''' Alternativ könntest Du auch den PC mehr Erfahrung aufsammeln lassen, indem Du nicht 20x sondern 2000x würfeln lässt. Nur ein paar Klicks! :-) | ||
| + | *[[Media: tk14.ods | TK14: Siedler von Catan - 2000x würfeln - Das Gesetz der großen Zahl]] | ||
| + | <br style="clear:left; "> | ||
| + | '''Merke:''' | ||
| + | Zufällige Ereignisse sind nicht vorhersehbar. Auf Dauer (im langjährigen Mittel) pendelt sich allerdings ihre Häufigkeit auf ihrer theoretischen Wahrscheinlichkeit ein (Gesetz der großen Zahl). | ||
| + | |||
| + | * Beim einfachen Würfelwurf pendelt sich jede Zahl in etwa auf 1/6 ein. | ||
| + | * Beim Siedler pendelt sich die Augensumme 2 etwa auf 1/40 ein, die 7 in etwa auf 1/6. Kann man das noch genauer klären, warum?! | ||
| + | * Die Verteilung (Das Bild des Histogramms) ähnelt einem Dreieck. Man nennt die Verteilung der Augensumme zweier Würfel daher auch die '''Dreiecksverteilung'''. | ||
===Aufgabe 4:=== | ===Aufgabe 4:=== | ||
| − | + | [[Datei: G_screenshotgaus5.png |thumb|links|300px|Screenshot: 5 Würfel Lösungsmuster]] | |
| − | * [[Media: | + | Was passiert bei der Augensumme von 5 Würfeln? |
| + | *'''TIPP:''' Probiere als Alternative zu einem Diagramm die Datenbalken (Format > Bedingte Formatierung > Datenbalken) | ||
| + | * [[Media: tk15.ods | TK14: Siedler von Catan - 2000x mit 5 Würfel würfeln - Der zentrale Grenzwertsatz]] | ||
| + | |||
| + | Die Augensumme von 5 Würfeln hängt nicht mehr von einer oder von zwei, sondern von fünf Ursachen ab. Das hat zur Konsequenz, dass die Verteilung nicht mehr dreiecksverteilt ist. Sie besitzt eine typische Wölbung, wie eine Glocke. Carl Friedrich Gauß (1777 - 1855) hat bewiesen (ohne Zuhilfenahme von Computern), dass alle '''natürlichen Ereignisse''', die von vielen, unabhängigen Ursachen abhängen, genau so verteilt sind. Diese Verteilung heißt daher auch '''Gauß'sche Normalverteilung''', ihr Histogramm heißt '''Gauß'sche Glockenkurve'''. | ||
| + | <br style="clear:left; "> | ||
| + | '''Merke:''' | ||
| + | Beeinflussen viele unabhängige Ursachen ein natürliches Ereignis, dann ist das Resultat immer verteilt wie die Gauß'sche Glockenkurve ([https://de.wikipedia.org/wiki/Zentrale_Grenzwerts%C3%A4tze zentraler Grenzwertsatz]). | ||
| + | |||
| + | '''Ergänzende Infos:''' | ||
| + | <gallery> | ||
| + | Datei: 10dm.jpg |10DM Schein zu Ehren von [https://de.wikipedia.org/wiki/Carl_Friedrich_Gau%C3%9F Carl Friedrich Gauß] | ||
| + | Datei: jahrgangsstufentestR6mathe2013.png |[http://jahrgangsstufenarbeiten.isb.bayern.de/download/14378/auswertung_mathematik_2013.pdf Jahrgangsstufentest Mathe R6 2013 - Auswerrtung von 35.866 Schüler:innen] | ||
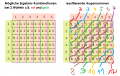
| + | Datei: beweisdreiecksverteilung.png | Analytischer Beweis, dass die Augensumme zweier Würfel dreiecksverteilt ist | ||
| + | </gallery> | ||
| + | |||
| + | Der analytische Beweis für den [https://de.wikipedia.org/wiki/Zentrale_Grenzwerts%C3%A4tze zentralen Grenzwertsatz] umfasst ein ganzes Buch! | ||
Aktuelle Version vom 17. Februar 2022, 17:44 Uhr
Wir nutzen die Tabellenkalkulation zur Simulation eines Zufallsexperiments und damit zur Klärung einer ernsten Forschungsfrage. Die These vieler erfahrener Siedlerspieler lautet: Beim Schicksalswürfeln (mit 2 Würfeln) kommen Augensummen in der Mitte (..., 6, 7, 8, ...) häufiger vor als extreme Augensummen (2, 3, ..., 11, 12). Mathefreaks wissen, ob das stimmt (durch sog. analytisches Denken). Wir wollen es einfach ausprobieren (die sog. empirische Methode)!
Wir lernen: Erzeugen von Zufallszahlen und damit Datenreihen, die reale Vorgänge simulieren. Wir lassen den PC Würfeln. Wir lernen Datenreihen mit der Funktion ZÄHLENWENN auszuzählen. Die Funktion neu berechnen (F9). Wir lernen Tricks zum Siedlerspielen, entdecken die Gaußsche Glockenkurve, das Gesetz der großen Zahl und den Zentralen Grenzwertsatz!
- TK12: Siedler von Catan - 20x würfeln - Lösungsmuster
- TK13: Siedler von Catan - 20x würfeln - Lösungsmuster perfekt formatiert
- TK14: Siedler von Catan - 2000x würfeln - Das Gesetz der großen Zahl
- TK15: Siedler von Catan - 2000x mit 5 Würfel würfeln - Der zentrale Grenzwertsatz
Aufgabe 1:
Lass Calc den PC 20x zwei Würfel werfen und stelle übersichtlich die Ergebnisse dar.
Überlege: Stimmt die Vermutung, dass 'mittlere Augensummen häufiger' vorkommen?
Drücke <F9> und lass den PC mehrmals würfeln. Was stellst Du fest?
Aufgabe 2:
Formatiere Deine Statistik sauber, anschaulich und übersichtlich - form follows function ;-). Achte auf folgende Punkte:
- Gliedernde Infos dominant - Ähnliches ähnlich - Verschiedenes verschieden ...
- Die Skala auf der y-Achse soll nicht immer hüpfen!
- TK13: Siedler von Catan - 20x würfeln - Lösungsmuster perfekt formatiert
Aufgabe 3:
Würfelt man nur 20x, dann ist kaum etwas Besonderes erkennbar. Vor allem ist es sehr stark vom Zufall abhängig (auch sonst im Leben kommen ja seltene Dinge vor - aber eben selten). Man kann also aus dem Vorkommen (bei 20x) nicht die Häufigkeit auf Dauer schließen. Seltene Ereignisse können sogar häufig vorkommen, aber es kommt eben selten vor, dass seltene Ereignisse häufig vorkommen. Was tun?!
- TIPP: Oft <F9> drücken und Erfahrung aufsammeln - wie erfahrene Spieler >>> Aufgabe 1!
- TIPP: Alternativ könntest Du auch den PC mehr Erfahrung aufsammeln lassen, indem Du nicht 20x sondern 2000x würfeln lässt. Nur ein paar Klicks! :-)
- TK14: Siedler von Catan - 2000x würfeln - Das Gesetz der großen Zahl
Merke:
Zufällige Ereignisse sind nicht vorhersehbar. Auf Dauer (im langjährigen Mittel) pendelt sich allerdings ihre Häufigkeit auf ihrer theoretischen Wahrscheinlichkeit ein (Gesetz der großen Zahl).
- Beim einfachen Würfelwurf pendelt sich jede Zahl in etwa auf 1/6 ein.
- Beim Siedler pendelt sich die Augensumme 2 etwa auf 1/40 ein, die 7 in etwa auf 1/6. Kann man das noch genauer klären, warum?!
- Die Verteilung (Das Bild des Histogramms) ähnelt einem Dreieck. Man nennt die Verteilung der Augensumme zweier Würfel daher auch die Dreiecksverteilung.
Aufgabe 4:
Was passiert bei der Augensumme von 5 Würfeln?
- TIPP: Probiere als Alternative zu einem Diagramm die Datenbalken (Format > Bedingte Formatierung > Datenbalken)
- TK14: Siedler von Catan - 2000x mit 5 Würfel würfeln - Der zentrale Grenzwertsatz
Die Augensumme von 5 Würfeln hängt nicht mehr von einer oder von zwei, sondern von fünf Ursachen ab. Das hat zur Konsequenz, dass die Verteilung nicht mehr dreiecksverteilt ist. Sie besitzt eine typische Wölbung, wie eine Glocke. Carl Friedrich Gauß (1777 - 1855) hat bewiesen (ohne Zuhilfenahme von Computern), dass alle natürlichen Ereignisse, die von vielen, unabhängigen Ursachen abhängen, genau so verteilt sind. Diese Verteilung heißt daher auch Gauß'sche Normalverteilung, ihr Histogramm heißt Gauß'sche Glockenkurve.
Merke:
Beeinflussen viele unabhängige Ursachen ein natürliches Ereignis, dann ist das Resultat immer verteilt wie die Gauß'sche Glockenkurve (zentraler Grenzwertsatz).
Ergänzende Infos:
10DM Schein zu Ehren von Carl Friedrich Gauß
Der analytische Beweis für den zentralen Grenzwertsatz umfasst ein ganzes Buch!