Hauptseite: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
| + | ===17. September 2020: MATHEMATIK AN EINER MÄDCHENSCHULE=== | ||
| + | <b>Eine Wortmeldung der Königsdisziplin - Ein Beitrag aus dem Jahresbericht 2004/2005</b> | ||
| + | |||
| + | [[Datei: noether.jpg |thumb|links|250px|Emmy Noether, *23. März 1882 in Erlangen, +14. April 1935 in den USA]] | ||
| + | |||
| + | <i>"Meine Mama hat gesagt, was sie in Mathe früher gelernt hat ('oder | ||
| + | auch nicht', Anm. des Autors), hat sie nie wieder gebraucht. Zu was | ||
| + | brauch ich dann dieses Mathe eigentlich?"</i> | ||
| + | |||
| + | Solche oder ähnliche Fragen sind das tägliche Brot eines Mathepaukers | ||
| + | an einer reinen Mädchenrealschule und sie spiegeln auch die allgemeine | ||
| + | Einstellung wieder, die in vielen Elternhäusern vorherrscht und die von | ||
| + | dort auch immer noch traditionell an Mädchen stärker weitergegeben | ||
| + | wird als an die Söhne der Familien. | ||
| + | |||
| + | Abgesehen davon, dass solche vielleicht tröstenden und daher gut gemeinten Kommentare für uns | ||
| + | als Pädagogen etwa eben so gelegen kommen wie ein ordentlicher Hagelsturm für den bemühten | ||
| + | Landwirt, sind sie mit großer Wahrscheinlichkeit ehrlich und damit subjektiv richtig. | ||
| + | Aber was sagen sie aus? Dass Mathematik im späteren Leben nicht gebraucht wird oder dass die | ||
| + | Kommentatorin in ihrem Leben bisher nicht die Gelegenheit ergriffen hat, sie zu gebrauchen? | ||
| + | Wer punktuell mit bestimmten Kompetenzen auf Kriegsfuss steht, versteht es bekanntlich blendend, | ||
| + | in seinem Leben um alles einen großen Bogen zu machen, was diese Kompetenzen erfordern | ||
| + | würde. Und dort, wo sich Handlungsfelder bieten würden, werden sie häufig nicht gesehen. Solche | ||
| + | Kommentare sind also eher Ausdruck eines geringen eigenen Bewegungsspielraums im späteren | ||
| + | Leben und dieser geringe Spielraum wird mit solchen Weisheiten sozusagen auf die nächste | ||
| + | Generation vererbt. | ||
| + | |||
| + | Die Optikerin, die sich das Aufbaustudium nicht zutraute, die Sozialpädagogin, die nie eine | ||
| + | verständliche Statistik über ihre Therapieerfolge machte, die OP-Schwester, die lieber den Tupfer | ||
| + | hält als neue technische Geräte zu bedienen, weil sie die Bedienungsanleitungen scheut, die | ||
| + | Unternehmerin, die ihre EXCEL-Tabellen und die Auswertungen der Geschäftszahlen außer Haus | ||
| + | gibt, ... Sie alle machen die - subjektiv richtige - Erfahrung, dass sie Mathematik nie brauchten. | ||
| + | |||
| + | Sollten sie alle diese Erfahrung an ihre Töchter weitergeben? | ||
| + | |||
| + | Mir persönlich geht es aber ... [[Mathematik an einer Mädchenschule | >>> mehr]] | ||
| + | |||
| + | <b>P.S.: Das Bild zeigt Emmy Noether (1882-1935), eine der bedeutendsten Mathematikerinnen des | ||
| + | 20. Jahrhunderts,</b> | ||
| + | |||
| + | <i>Wolfgang Lentner</i> | ||
| + | |||
| + | <br style="clear:left; "> | ||
| + | |||
===21. November 2023: Eine Reaktion auf eine Beobachtung zum Schülerprojekt "Buchstabe O" (siehe unten)=== | ===21. November 2023: Eine Reaktion auf eine Beobachtung zum Schülerprojekt "Buchstabe O" (siehe unten)=== | ||
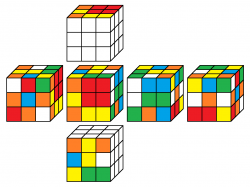
[[Datei: Rubikbild3.png |thumb|links|250px|Punktemuster am RUBIK-Cube]] 2023 hielt Prof. Dr. Simon Lentner an der Uni Hamburg ein Seminar für Lehramtsstudenten zum Thema Gruppentheorie/RUBIK-Würfelmuster. Ausgangspunkt war die Beobachtung aus >>> [[CUBE.CODES: Buchstabe O]], dass die 6 ungeklärten Bilder nicht im Orbit des Orginalwürfels liegen, also nicht mit Moves davon erreichbar sind und die verbleibenden (scheinbar völlig zufälligen) 8 bei genauerem Hinsehen aus dem einen veröffentlichten Zug zu bewerkstelligen sind, indem man einfach den Zug auf allen 4 Raumdiagonalen 1x oder 2x anwendet. Die Studenten diskutierten dort, warum alle Lösungen (bis auf Drehungen um die Raumdiagonalen) eigentlich Varianten eines einzigen Typs sind. Sollte das Zufall sein? Wie sieht dies bei anderen Mustern aus? [[Media: rubiksimon.pdf | Veröffentlichung der Diskussion an der Uni Hamburg]]<p> | [[Datei: Rubikbild3.png |thumb|links|250px|Punktemuster am RUBIK-Cube]] 2023 hielt Prof. Dr. Simon Lentner an der Uni Hamburg ein Seminar für Lehramtsstudenten zum Thema Gruppentheorie/RUBIK-Würfelmuster. Ausgangspunkt war die Beobachtung aus >>> [[CUBE.CODES: Buchstabe O]], dass die 6 ungeklärten Bilder nicht im Orbit des Orginalwürfels liegen, also nicht mit Moves davon erreichbar sind und die verbleibenden (scheinbar völlig zufälligen) 8 bei genauerem Hinsehen aus dem einen veröffentlichten Zug zu bewerkstelligen sind, indem man einfach den Zug auf allen 4 Raumdiagonalen 1x oder 2x anwendet. Die Studenten diskutierten dort, warum alle Lösungen (bis auf Drehungen um die Raumdiagonalen) eigentlich Varianten eines einzigen Typs sind. Sollte das Zufall sein? Wie sieht dies bei anderen Mustern aus? [[Media: rubiksimon.pdf | Veröffentlichung der Diskussion an der Uni Hamburg]]<p> | ||
| Zeile 202: | Zeile 246: | ||
<i>Euer Wolfgang Lentner</i> | <i>Euer Wolfgang Lentner</i> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br style="clear:left; "> | <br style="clear:left; "> | ||
Version vom 8. September 2024, 18:34 Uhr
17. September 2020: MATHEMATIK AN EINER MÄDCHENSCHULE
Eine Wortmeldung der Königsdisziplin - Ein Beitrag aus dem Jahresbericht 2004/2005
"Meine Mama hat gesagt, was sie in Mathe früher gelernt hat ('oder auch nicht', Anm. des Autors), hat sie nie wieder gebraucht. Zu was brauch ich dann dieses Mathe eigentlich?"
Solche oder ähnliche Fragen sind das tägliche Brot eines Mathepaukers an einer reinen Mädchenrealschule und sie spiegeln auch die allgemeine Einstellung wieder, die in vielen Elternhäusern vorherrscht und die von dort auch immer noch traditionell an Mädchen stärker weitergegeben wird als an die Söhne der Familien.
Abgesehen davon, dass solche vielleicht tröstenden und daher gut gemeinten Kommentare für uns als Pädagogen etwa eben so gelegen kommen wie ein ordentlicher Hagelsturm für den bemühten Landwirt, sind sie mit großer Wahrscheinlichkeit ehrlich und damit subjektiv richtig. Aber was sagen sie aus? Dass Mathematik im späteren Leben nicht gebraucht wird oder dass die Kommentatorin in ihrem Leben bisher nicht die Gelegenheit ergriffen hat, sie zu gebrauchen? Wer punktuell mit bestimmten Kompetenzen auf Kriegsfuss steht, versteht es bekanntlich blendend, in seinem Leben um alles einen großen Bogen zu machen, was diese Kompetenzen erfordern würde. Und dort, wo sich Handlungsfelder bieten würden, werden sie häufig nicht gesehen. Solche Kommentare sind also eher Ausdruck eines geringen eigenen Bewegungsspielraums im späteren Leben und dieser geringe Spielraum wird mit solchen Weisheiten sozusagen auf die nächste Generation vererbt.
Die Optikerin, die sich das Aufbaustudium nicht zutraute, die Sozialpädagogin, die nie eine verständliche Statistik über ihre Therapieerfolge machte, die OP-Schwester, die lieber den Tupfer hält als neue technische Geräte zu bedienen, weil sie die Bedienungsanleitungen scheut, die Unternehmerin, die ihre EXCEL-Tabellen und die Auswertungen der Geschäftszahlen außer Haus gibt, ... Sie alle machen die - subjektiv richtige - Erfahrung, dass sie Mathematik nie brauchten.
Sollten sie alle diese Erfahrung an ihre Töchter weitergeben?
Mir persönlich geht es aber ... >>> mehr
P.S.: Das Bild zeigt Emmy Noether (1882-1935), eine der bedeutendsten Mathematikerinnen des 20. Jahrhunderts,
Wolfgang Lentner
21. November 2023: Eine Reaktion auf eine Beobachtung zum Schülerprojekt "Buchstabe O" (siehe unten)
2023 hielt Prof. Dr. Simon Lentner an der Uni Hamburg ein Seminar für Lehramtsstudenten zum Thema Gruppentheorie/RUBIK-Würfelmuster. Ausgangspunkt war die Beobachtung aus >>> CUBE.CODES: Buchstabe O, dass die 6 ungeklärten Bilder nicht im Orbit des Orginalwürfels liegen, also nicht mit Moves davon erreichbar sind und die verbleibenden (scheinbar völlig zufälligen) 8 bei genauerem Hinsehen aus dem einen veröffentlichten Zug zu bewerkstelligen sind, indem man einfach den Zug auf allen 4 Raumdiagonalen 1x oder 2x anwendet. Die Studenten diskutierten dort, warum alle Lösungen (bis auf Drehungen um die Raumdiagonalen) eigentlich Varianten eines einzigen Typs sind. Sollte das Zufall sein? Wie sieht dies bei anderen Mustern aus? Veröffentlichung der Diskussion an der Uni Hamburg
Wer gerne alle Arten mal mathematisch verstehen möchte, auf die man den Würfel in die Hand nehmen kann, der sollte mal die folgende Seite ansehen: >>> Die Symmetriegruppe des RUBIK-Würfels
Die meisten Forschungsfragen (welche Farbvarianten von Muster es gibt) sind noch ungeklärt! Auf geht's!
24. Juni 2023: Ein Zoom ins Apfelmännchen
>>> Pink Floyd: shine on your crazy diamonds
>>> Video-Zoom
24. Juni 2023: Schaffkopf: Mit etwas Glück und ...
>>> Und jedem Anfang wohnt ein Zauber inne, ...
in memoriam Oscar, my favorite Math-Teacher
24. Juni 2023: MML 2023 an der Ludwig-Maximilian-Universität München
2023 stellte ich an der LMU München einen weiten Fragenkreis um offene Probleme beim RUBIK-Würfel vor.
Im Netz wimmelt es von Seiten (und Zügen), mit denen man bestimmte Muster am RUBIK-Würfel von der Lösungsposition aus herstellen kann. Einige dieser Seiten diskutieren auch ansatzweise Farbvarianten solcher Grundmuster, ohne das allerdings erschöpfend zu klären, welche Farbvarianten es geben könnte. Wie uferlos das schon beim einfachsten Muster sein kann und wie schnell man mitten in der spannendsten Mathematik sein kann, wollte mein diesjähriger Workshop zeigen. Da ich von Jahrgangsstufe 6 bis 11 ein buntes Publikum hatte mit Cubern und ohne Cube-Vorwissen, brachte ich viele Materialien mit und verließ mich auf einen spannenden spontanen Dialog. Am Ende streiften wir noch die trügerische Illusion, dass man mit Zügen von der Lösungsposition aus alle Stellungen herdrehen kann. Schon bei einfachen Zügen wie "ER" sieht man, dass man sich bei der Wiederholung und Kombination immer auf einem "gewissen Orbit" von Stellungen bewegt, aus dessen Dunstkreis man nie herauskommt. Spätestens ab dieser Erkenntnis sollte man sich einmal fragen, ob nicht doch die "Gruppentheorie" eine passende Grundlage für die Beschäftigung mit dem Cube sein könnte! ...
Ein Großteil der Fragen (und teilweise Antworten) ist in der folgenden Unterrichtsdoku gestreift: >>> CUBE.CODES: Buchstabe O
10. April 2022: Diener des Volkes - ARTE Serie
Wolodymyr Selenskyj ist Präsident der Ukraine und wurde am 31. März 2019 mit 73% der abgegebenen Stimmen gewählt. Wenige wissen, dass er zuvor Schauspieler und Komiker war.
2015 drehte er eine Filmserie, indem er einen Geschichtslehrer spielt, der in der Ukraine Präsident wird. Darin karikiert er nicht nur Amt und Land sondern streut auch immer wieder Seitenhiebe auf den großen Bruder Russland ein. 4 Jahre später sind ihm die Herzen der Ukrainer zugeflogen und er wurde tatsächlich der, den er noch 4 Jahre vorher im Film spielte! Seine Beliebtheit und seine überzeugende Art für Menschlichkeit, Wahrhaftigkeit und Freiheit einzutreten, seine Tapferkeit und Unerschütterlichkeit berühren immer mehr Menschen auf dieser Erde. Diese Beliebtheit beim Volk hat ihm den Hass des russischen Präsidenten eingetragen. Eben wird er und sein Land zu Tode gehetzt. Ich fürchte jeden Tag um sein Leben!
PS: Seit einigen Tagen ist die Serie leider nicht mehr in der ARTE-Mediathek. Es ist aber möglich, die Folgen in YOUTUBE mit Werbung anzusehen!
26. Oktober 2022: MINT-Fortbildung an der Staatlichen Realschule Bruckmühl, Tetris, Soma, Rumis & Co
Tetris, Soma, Rumis & Co sind allesamt Spiele, die mit 2D- oder 3D-Polyquadraten/-würfeln mathematische Packungsprobleme behandeln. Sie fordern alle drei Lehrplanthemen der 5. Klasse (Mathematik) und schulen durch die Kombination aus natürlicher, spielerischer Motivation und haptischem Fordern die Entwicklung von kombinatorischem Denken und räumlichem Vorstellungsvermögen.
Lehrplanthemen:
- systematisches Abzählen (Baumdiagramm)
- Volumenrechnung mit Quadern und Polywürfeln (auch zeichnen)
- Teilbarkeit, Primfaktorzerlegung
>>> MINT-Fortbildung an der Staatlichen Realschule Bruckmühl, 26. Oktober 2022, Tetris, Soma, Rumis & Co
>>> ... Weitere Fortbildungsdokus für Lehrer:innen
Die Fortbildungsunterlagen sind stark zusammenfassend und eher nur für Leher als Zielgruppe gedacht.
26. Oktober 2022: MINT-Fortbildung an der Staatlichen Realschule Bruckmühl, mit PIVOT-Stickfigure-Manager digitale Daumenkinos erstellen
Im Modul IT 2.8.2 des Lehrplans IT PLUS erstellen wir mit Schüler:innen u.a. digitale Daumenkinos. Verteilt man die beiden Inhalte "pixelorientierte Techniken" und "objektorientierte Techniken" in etwa gleich auf die zur Verfügung stehenden 14 Wochenstunden und berücksichtigt evtl. Leistungserhebungen, dann bleiben Möglichkeiten übrig, die professionelle Programme völlig ausschließen. Der PIVOT Animator in seiner orginalen Version 2.2.7 trifft da genau das passende Niveau!
>>> MINT-Fortbildung an der Staatlichen Realschule Bruckmühl, 26. Oktober 2022, Mit PIVOT-Stickfigure-Manager digitale Daumenkinos erstellen
>>> ... Weitere Fortbildungsdokus für Lehrer:innen
1. Oktober 2022: Matheprojekt: Würfel färben 1*6
Einen Würfel mit drei Farben anzumalen (sagen wir in rot-gelb-blau), ist sicherlich nicht schwer. Da man dabei 6 mal die Entscheidung hat, ihn rot, gelb oder blau anzumalen, geht das zunächst mal auf $$3^6=729$$ verschiedene Arten, vorausgesetzt, man hat die Freiheit, jede Farbe beliebig oft benutzen zu können oder nicht, es also auch einfarbige Würfel geben darf. Da aber jeder Mensch Würfel als eigentlich gleich gefärbt betrachtet, wenn sie sich nur durch Drehung voneinander unterscheiden, sind es eigentlich viel weniger als 729???! Ein schönes Projekt mit einer 5. oder 6. Klasse ...
17. September 2022: Matheprojekt: Würfel färben 4*6
Könnt Ihr zählen? In der Zeitschrift MATHE-LMU.DE des Fördervereins der Mathematischen Fakultät der LMU war folgende Rätselaufgabe zu lesen:
Ein Würfel, dessen Seitenflächen jeweils aus vier Quadraten bestehen, wird in den Farben rot, blau und gelb eingefärbt. Die kleinen Teilquadrate sollen aber so gefärbt sein, dass (wie bei einer Landkarte) angrenzende Flächen (angrenzende Länder) keine gleichen Farben tragen. Wie viele Quadrate werden in den jeweiligen Farben gefärbt? (Das Titelbild der Zeitschrift seht ihr nebenan. Man hat die Rückseite des Würfels nicht einmal gesehen!)
Professor Steinlein war etwas verärgert, eine so kindisch einfache Aufgabe (Seht Ihr die Antwort auf einen Blick?) in der Rätselecke der Zeitschrift seiner Universität zu finden. Und so fragte er in der nächsten Ausgabe weiter: Wie viele verschiedene solche Würfel gibt es denn?
Ob ihm die Schwierigkeit dieser Frage beim Fragen schon bewusst war? Auf jeden Fall musste er sich zur Beantwortung seiner eigenen Frage schon selbst ein paar Wochen zurückziehen. Heraus kam nicht nur eine schöne Lösung (eine ausgewachsene Forschungsarbeit über zig Seiten), sondern ein teilweise wunderschöner kombinatorischer Gedankengang, der für alle Schüler der Sekundarstufe nicht nur nachvollziehbar, sondern auch in weiten Teilen experimentell selbst zu entdecken ist.
Außerdem ist die Arbeit ein sehr schönes Beispiel, wie uferlose Abzählprobleme durch raffiniertes Strukturieren auf einmal übersichtlich und einfach werden. Der mögliche händisch-experimentelle Zugang schult in hervorragender Weise das räumliche sowie das kombinatorische Denken. Die Möglichkeit, einige hölzerne Fälle arbeitsteilig anzugehen, macht sie zu einer sehr schönen Forschungsfrage für Schulklassen auf einer Mathematikfreizeit.
Alternative Motivation: Steht ein ungefärbter Würfelklotz (z.B. aus Holz) vor mir, kann ich ihn auf 3 hoch 24 = 282.429.536.481 Arten mit drei Farben einfärben. Dann gibt es aber viele Flächen nebeneinander, die gleich farbig sind (vgl. politische Landkarte). Nicht schön! Bei wie vielen von den 282.429.536.481 kommt dies Unschöne nicht vor (also nur verschiedenfarbige Nachbarländer)? Schätzen!
Empfohlene Zeit:
- Für eine vollständige Lösung durch Schüler mit dem Polyederbaukasten POLYDRON zwei ganze Tage.
- Auch Teillösungen an einem Projekttag sind interessant.
- Lässt man Schüler selber forschen und unterstützt alternative Lösungsansätze der Schüler, kann auch gut eine Projektwoche mit der Aufgabe gestaltet werden. (Brute-force-Strategien evtl. mit PC-Unterstützung mittels Tabellenkalkulation oder prozeduraler Programmierung)
Vorwissen: Gleichungen formulieren, umformen und einsetzen.
Wolfgang Lentner
11. September 2022: Informationtechnologie an der R6 Bayern
>>> IT Lehrplan PLUS - Umsetzung an der Städtischen Realschule für Mädchen Rosenheim
BB3: Bildbearbeitung - Eigenes Memoryspiel gestalten (Bildbearbeitung/html/JavaScript)
An einem schönen Beispiel sieht man einmal, wie in der Wirklichkeit (beim WEB-Design) Bildbearbeitung, html-Gestaltung und JavaScript-Programmierung ineinander greifen können. So können wir von der 7. Klasse bis rauf zur 10. Klasse ein eigenes kleines Internet-Projekt verwirklichen. Als Motivation für die nächsten Jahrgänge sind in der folgenden Galerie einige Schülerinnen-Arbeiten ausgestellt. Viel Spaß dabei!
>>> Zur Memory-Übersichtsseite
BB2: Retuscheübung - 10 Fehlersuchbilder
Suche Dir ein geeignetes Bild im Internet und bearbeite es in MS Paint zu einem 10-Fehler-Suchbild. Sieh' Dir zuerst die Bilder aus der Schülergalerie an und überlege, welche Fehler für die Ratenden witzig, spannend oder langweilig sind.
>>> Zur Galerie
BB1: Lernumgebung RUBIK-Rätselgrafiken
- Rätselaufgabe für ein Zeitschrift - Beispiel - Ich bin das Rätselkind - erstmal in's Problem eindenken
- Rätselaufgaben selber entwerfen - Ich bin der Autor - mit fertigen Grafiken umgehen, fertige Grafiken bearbeiten
- Grafiken entwerfen - Ich bin der Illustrator/Werbegrafiker - wie kann ich mit Paint so eine Grafikvorlage überhaupt entwerfen
- Die Zeitschrift gestalten - Ich bin der Chefredakteur - Datenaustausch: Textverarbeitung <> Paint
>>> zu den Aufgabenvorschlägen
>>> zu den Lösungsvorschlägenen
17. Oktober 2021: Tabellensammlung (ods-Format)
29. Oktober 2022: RUBIK-Mosaike (8x10 Würfel)
>>> RUBIK-Mosaike (8x10 Würfel), Ausstellungsstücke von Schülerinnen
23. Juni 2021: Programmierung an der R6 Bayern
>>> Zur Übersicht über meine Unterrichtsmaterialien zum Thema Programmierung
7. Februar 2021: Katherine Maher tritt ab
Personen in der ARTE-Doku über WIKIPEDIA
20. Januar 2021: Forscherklasse 5b, Türme von Hanoi
https://www.mathematik.ch/spiele/hanoi_mit_grafik/
15. Januar 2021, WIKIPEDIA feiert seinen 20. Geburtstag, die ARTE-Doku zum WIKIPEDIA-Internet-Projekt
Wikipedia ist eines der interessantesten und wichtigsten Internetprojekte der Weltgeschichte. Die Doku spricht ganz viele aktuelle Aspekte des Projekts an. Seht Euch diese Woche mal den Film an (am besten gleich mit der ganzen Family). Nebenbei berührt der Film auf perfekte Art wichtige Punkte unseres Lehrplans in drei Jahrgangsstufen durch die Themen ...
- IT 1.4 Informationsaustausch (ca. 14 Std.)
- IT 1.7 Informationsbeschaffung und -präsentation (ca. 14 Std.)
- IT 1.8 Grundlagen elektronischer Datenverarbeitung (ca. 14 Std.)
- IT 2.5.2 Datennetze II (ca. 14 Std.)
>>> Auf der Geburtstagsseite: 15. Januar 2021, WIKIPEDIA hat Geburtstag gibt es nebenbei noch viele weitere Infos zu WIKIPEDIA
21. Dezember 2020: Weihnachtsrätsel der TH Rosenheim
Viel Spaß bei diesem klasse Rätsel (und Danke an die Autoren! :-))
https://youtu.be/uU7y7Jbk0H8
Wer Tabellenkalkulationsfan ist, kann sich noch folgenden Tipp ansehen ...
HINT für OpenOffice-Fans
Ich hoffe sehr, dass es Allen gut geht und möchte Euch ein besonders schönes Weihnachtsfest in diesem Jahr wünschen,
Euer Wolfgang Lentner
17. September 2020: RUBIK-Videos auf dem MINT-Wiki
Wer noch kein Weihnachtsgeschenk hat, kann vielleicht mit dem berühmten WÜRFEL-PUZZLE des Herrn Rubik für den Lockdown punkten :-)!!!
Hier im MINT-WIKI gibt's eine YouTube-Video-Strecke (16 Videos) zum Lösen des Würfels
Viel Spaß und unterhaltsame Ferien mit oder ohne Würfel :-)
Euer Wolfgang Lentner