SJ 21/22: Klasse 9b

Kaufmännischer Zweig (zweistündig - IT Wahlpflichtfächergruppe II)
Bezeichnung in der SchulApp: IT_1/9b_2
>>> zurück zur Klassenübersicht

Ausgewählte Themenblöcke

• Themenblock: IT 2.2.2 Tabellenkalkulation II (ca. 14 Std.) (Wahlmodul)
  • Media: Klassenstatistik.ods
  • Media: Klassenstatistik2.ods
  • Media: Prozentrechnen Grundaufgaben2.ods
  • Media: Prozentrechnen Grundaufgaben.ods
  • Media: Einkaufskalkulation.ods
  • 10.11.2021, 1. Stegreifaufgabe: Prozentrechnen
  • Media: Ex Prozentrechnen Grundaufgaben.ods
  • Media: Ex Prozentrechnen Grundaufgaben ml.ods
  • Media: Ex Prozentrechnen Grundaufgaben angabe.odt
  • Media: Tilgungsplan jährlich 2.ods
• Themenblock: TXT1: Der tabellarische Lebenslauf
• Projektarbeit:
  • BODY-Painting - Johannes Stöttner
  • Leitfach Deutsch: Herr Maier

Projekt

• Email: https://web.de/ Account: 9bmrs@web.de Passwort: emailadresse-wirsindhelden-hallo
• Abdobe Express: https://www.adobe.com/de/express/ Account: 9bmrs@web.de Passwort: 9bProjekt-wirsindhelden-hallo
• Projektbewertungen: Media: Projektbewertungen9b.odt

Themenblock: IT 2.6.1 Modellieren und Codieren von Algorithmen (ca. 14 Std.)

• CUBE.CODES
• 3.12.: RUBIK-Würfel erforschen - erste Ebene
• 10.12.: Wie viele fixpunktfreie Permutationen der Länge 4 gibt es?
• 10. Januar: RUBIKs Challange

>>> CUBE.CODES blank
>>> Erste Schritte
>>> CUBE.CODES: Einfache EVA-Programme
>>> CUBE.CODES: Beispiele aus der Zahlentheorie (Klasse 5)
>>> CUBE.CODES: Schleifen mit while
>>> CUBE.CODES: Schleifen mit for
>>> CUBE.CODES: Rekursion

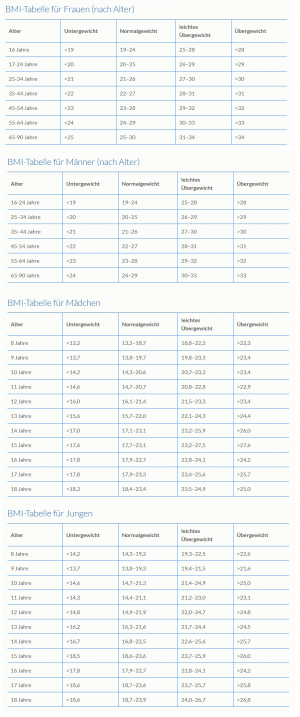
• 6. April: Hausaufgabe 1 von drei EVA Programmen (BMI)

https://ide.cube.codes/?init=loadFromUrl&url=https://share-repository.cube.codes/v1/appStates/20e6932d-64b7-4fe0-9651-fdd4a4828d7e

x=1;
while(x<=80) {
   await CUBE.move(" R B L F ");
   ++x;
}

Wie lang dauert es, bis der CUBE wieder solved ist?

harry=1;
await CUBE.move(" R B L F' ");
while(!CUBE.isSolved()) {
 ++harry;
 await CUBE.move(" R B L F' ");
}
UI.log(harry);

oder eleganter ...

harry=0;
do {
   await CUBE.move(" R F' ");
   UI.log(++harry);
} while(!CUBE.isSolved())

zahl=400;
teiler=17;
if(zahl%teiler==0) 
    UI.log("geht auf"); 
else 
    UI.log("geht nicht auf");

Größte Primzahl

zahl=4033343771;
teiler=1;
while(teiler<=zahl) {
   if(zahl%teiler==0) UI.log(teiler); 
   ++teiler;
   }

ca. 2,5 Minuten

CUBE.CODES: Buchstabe O

Tunig

• Gegenteilertrick
• Hausi: Teiler von 550 mit Gegenteilertrick